Контакты

Случайная статья

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 17. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. Вычисление длины дуги кривой

Стр 1 из 2Следующая ⇒

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 17

ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Вычисление площадей

Площадь криволинейной трапеции, ограниченной сверху

кривой y=f(x), вертикалями x=a, x=b и осью OX, определяется как

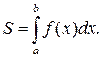
1. Вычислить площадь, ограниченную параболой y= 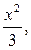прямыми x=2, x=3 и осью абсцисс.

Здесь площадь

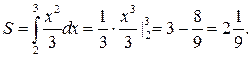
2. Вычислить площадь, ограниченную кривой y=lnx, осью OX и прямой x=e.

В данном случае

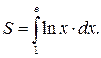Этот интеграл нужно вычислять по частям. Положим u=lnx, dv=dx. Тогда

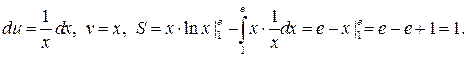
3. Вычислить площадь, ограниченную одной полуволной синусоиды y=sinx и осью OX. Здесь

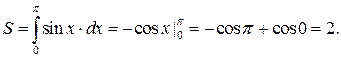
4. Найти площадь, ограниченную параболами

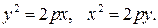
Определим точки пересечения парабол. У нас

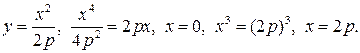
Следовательно, площадь

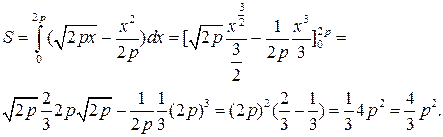
5. Вычислить площадь, заключенную между локоном

Аньези 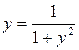и параболой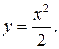

Точки пересечения кривых найдем из равенства

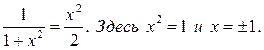
Тогда площадь

6. Найти площадь, ограниченную осью OX и одной аркой циклоиды x=a(t-sint), y=a(1-cost).

Здесь при x=0 t=0; при x=2πa t=2π, dx= a(1-cost).

При переходе к новой переменной получим, что

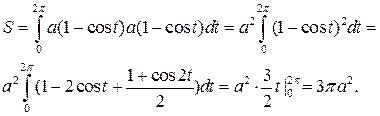
Площадь в полярных координатах для кривой 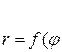находится по формуле

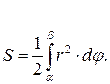
7. Найти площадь, ограниченную кривой

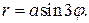
Это трехлепестковая роза. Длина одного лепестка найдется при 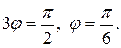Это будет а. Он находится между 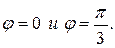Для трех лепестков

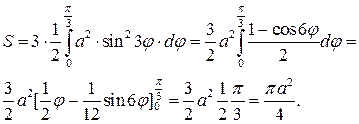
Вычисление длины дуги кривой

Длина кривой y=f(x) между точками x=a, x=b находится по формуле

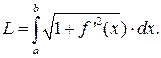
1. Вычислить длину дуги полукубической параболы

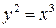от начала координат до точки (4, 8).

Здесь

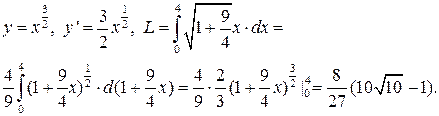
Если кривая в полярных координатах задана как

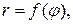то длина дуги

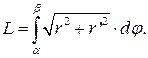
2. Найти длину первого витка спирали Архимеда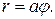

В этом случае 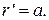Угол φ вначале равен 0, после первого витка 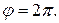Таким образом,

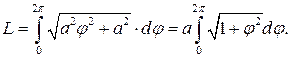
Дальше вычисление проведем с помощью известного интеграла:

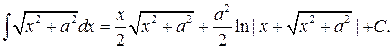
Тогда

12 Следующая ⇒

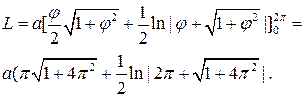
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.