Ранг матрицы. Решение системы линейных уравнений матричным методом. Метод Гаусса

Ранг матрицы

Рангом матрицы называется наибольший из порядков отличных от нуля ее миноров.

Ранг может быть равен 1,2,3,…

6.Например, если в матрице 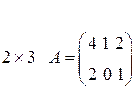хотя бы один из определителей второго порядка , полученный путем зачеркивания одного столбца, не равен нулю, то ранг матрицы равен двум. Здесь, в частности,

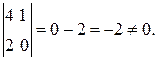Ранг матрицы равен двум.

При нахождении ранга матрицы обычно применяют так называемые элементарные преобразования.

7. Определить ранг матрицы

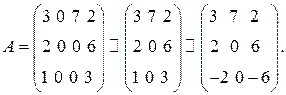
Здесь сделали два преобразования: вычеркнули второй нулевой столбец и третью строку умножили на -2. Затем к второй строке прибавим третью и вычеркнем третью нулевую строку:

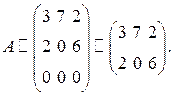
В полученной матрице можно получить три определителя второго порядка путем зачеркивания столбцов и все они не будут равны нулю. Значит, ранг этой матрицы r(A)=2.

Решение системы линейных уравнений матричным методом

Давайте решим этим методом систему из примера 4.

8. Обозначим

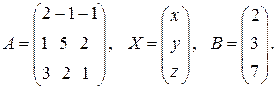
Тогда наша система в матричном виде запишется как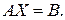

Ее решением будет 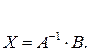Обратная матрица для этого случая была нами найдена в примере 5. Тогда

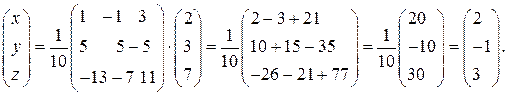
Отсюда получаем: x=2, y=-1, z=3.

Метод Гаусса

Его называют также методом последовательного исключения. Рассмотрим 2 способа решения в этом случае.

9. Решить систему

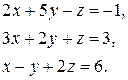
Здесь нужно, чтобы в первом уравнении перед первой неизвестной была 1. Если это не 1, то на этот коэффициент делят все первое уравнение. Чтобы избежать вычислений с дробями, давайте поменяем местами первое и третье уравнения. Тогда система примет вид:

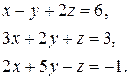Исключим x из второго и третьего уравнений. Для этого первое уравнение умножим на -3 и сложим со вторым, затем первое уравнение умножим на -2 и прибавим к третьему. После этого получим 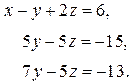Сократим на 5 второе уравнение

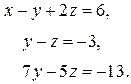
Исключим у из третьего уравнения. Для этого умножим второе уравнение на -7 , прибавим к третьему и получим

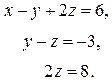Окончательно треугольный вид системы примет следующую форму:

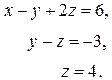
Мы осуществили прямой ход метода Гаусса. Решения системы находятся обратным ходом: z=4, y=z-3=1, x=y-2z+6=-1. Данная система является совместной и определенной.

10. Решим следующую систему с помощью расширенной матрицы и элементарных преобразований по Гауссу:

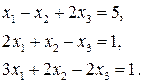
Составим расширенную матрицу, затем первую строку умножим на -2 и прибавим ко второй, первую строку умножим на -3 и прибавим к третьей, в следующей записи вторую строку умножим на 2:

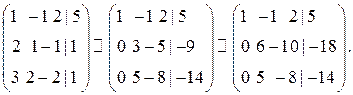
Дальше от второй строки отнимаем третью, чтобы вместо 6 получить 1, вторую строку умножаем на -5 и прибавляем к третьей, в последней записи третью строку сокращаем на 2:

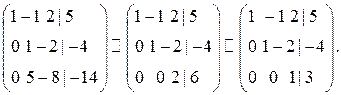
Полученная матрица соответствует системе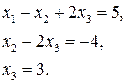

Это прямой ход метода, обратным ходом находим:

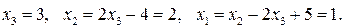
Если в последней строке, например вместо 1, стоит 0, то уравнение системы становится противоречивым, система не совместна и не имеет решения.

⇐ Предыдущая 12