Контакты

Случайная статья

Экстремумы функции

⇐ ПредыдущаяСтр 2 из 2

Экстремумы функции

Найти промежутки возрастания и убывания функций.

1. Пусть Ее о.д.з. 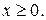Производная

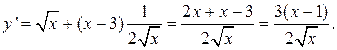
Она равна нулю y’=0 при x=1. Здесь будет два интервала:

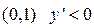функция убывает,

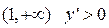функция возрастает.

При х=1 производная меняет знак с - на +, поэтому при х=1 функция имеет минимум, который равен -2. При построении графика здесь нужно учесть, что у=0 при х=0 и х=3.

Исследовать на экстремум следующие функции.

2. Возьмем 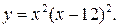Ее производная

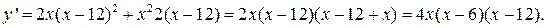
Она равна нулю, y’=0 при х=0, х=6, х=12. Получим следующие интервалы:

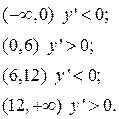
Отсюда видим, что при х=0 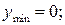при х=6

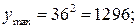при х=12 При построении графика нужно учесть, что у=0 при х=0 и х=12.

3. Пусть 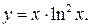О.д.з. этой функции x>0.

Производная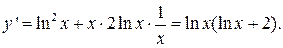

Ищем критические точки:

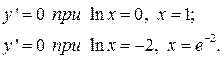
Составим интервалы

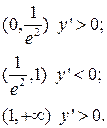
Отсюда получим, что при

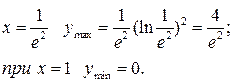
При построении графика нужно учесть, что

Рассмотрим текстовые задачи.

4. Кусок проволоки данной длины L согнуть в виде прямоугольника так, чтобы площадь последнего была наибольшей.

Возьмем прямоугольник со сторонами х и у. Его площадь S=xy. Периметр L=2x+2y. Тогда

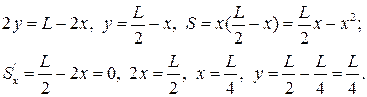
Таким образом, этот прямоугольник должен быть квадратом со стороной L/4.

5. Открытый жестяной бак с квадратным основанием должен вмещать V литров. При каких размерах на изготовление бака потребуется наименьшее количество жести.

Обозначим сторону основания бака через х, а высоту через у. Тогда площадь поверхности будет

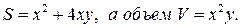
Отсюда

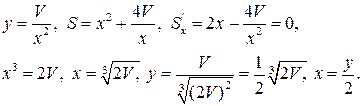
Высота должна быть в два раза меньше стороны основания.

Задание на дом.

В данный шар радиусом R вписать цилиндр

с наибольшим объемом.

Вначале в окружность впишите прямоугольник.

Ответы по цилиндру:

высота 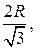радиус основания

⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.