Хелпикс

Главная

Контакты

Случайная статья



ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 11. ДИФФЕРЕНЦИАЛ ФУНКЦИИ. Производные высших порядков. Дифференциал функции. Правило Лопиталя

Стр 1 из 2Следующая ⇒


ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 11

ДИФФЕРЕНЦИАЛ ФУНКЦИИ

                    Производные высших порядков

Производной второго порядка функции y=f(x)  называется производная от ее первой производной, т.е. y’’=(y’)’.

Ее записывают также как  f’’(x) или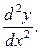    

 Для n-ой производной будут такие обозначения:

                       

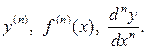
Найти производные второго порядка от следующих функций.

1. 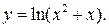  Здесь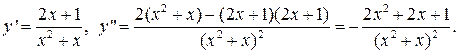

 

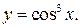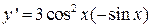2.    Тогда    и

 

 

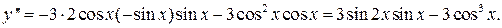
3.Найти n-ую производную от функции 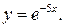  Здесь

    

 

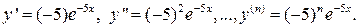
                       Дифференциал функции

Для функции y=f(x) дифференциал функции определяется как  dy=f’(x) dx.  Найдем дифференциалы нескольких функций.

1. Пусть 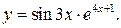   Тогда

 

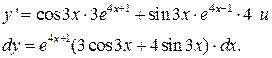
2. Возьмем 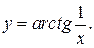   В этом случае

 

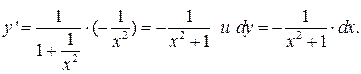
Обычно дифференциал применяют в приближенных вычислениях. Поскольку приращение функции мало отличается от значения дифференциала, то можно применить формулу

           

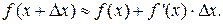
3. Вычислить 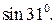  Вначале идет выбор функции, у нас

f(x)=sinx   и, следовательно,  f’(x)=cosx. Пусть  

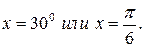Тогда 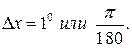 Окончательно

 

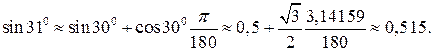
                Правило Лопиталя

Оно применяется для раскрытия неопределенностей

вида 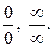    В этом случае 

              

 

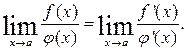
1. Найти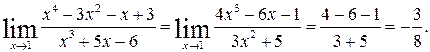

 

2. Возьмем 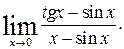  Дифференцируя числитель и знаменатель, получим предел

 

 

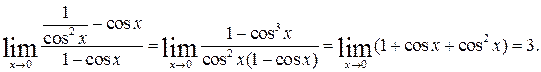
3.

 

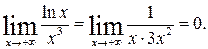
Неопределенности вида  

         

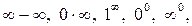
как правило, сводятся к предыдущим двум.

 

4.  Найти 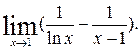  Это неопределенность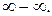

Приведем здесь дроби к общему знаменателю:

 

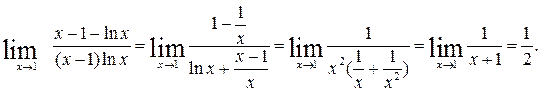
5. Рассмотрим случай 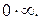   Найдем 

 

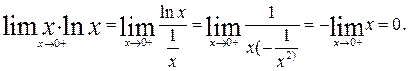
6.

 

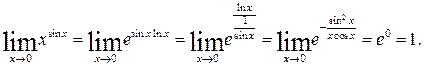
7.

 


12Следующая ⇒
  

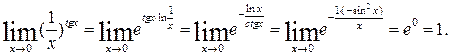
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.