
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа 15. по теме: «Тригонометрические уравнения и неравенства. с геометрической интерпретацией». Материал к практической работе. Определения арксинуса, арккосинуса, арктангенса и. арккотангенса числового аргумента.
Практическая работа 15
по теме: «Тригонометрические уравнения и неравенства
с геометрической интерпретацией»
Цель работы:
1) отработать навыки работы с таблицей значений тригонометрических функций;
2) закрепить навыки применения тригонометрических формул при вычислении значений тригонометрических функций и преобразовании выражений, содержащих тригонометрические функции;
3) отработать навыки решения тригонометрических уравнений и неравенств с использованием тригонометрического круга.
Выполняя данную работу, студент должен знать:
· формулы тригонометрии;
· формулы корней простейших тригонометрических уравнений;
· методы решения простейших тригонометрических неравенств.
уметь:
· различать тригонометрические формулы;
· применять тригонометрические формулы при преобразовании выражений;
· решать тригонометрические уравнения и неравенства.
Ход работы:
1. Изучить материал по теме практической работы.
2. Выполнить задания практического материала.
Материал к практической работе
Определения арксинуса, арккосинуса, арктангенса и
арккотангенса числового аргумента.
Определение. Арксинусом числа х называется число из отрезка 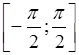 , синус которого равен х.
, синус которого равен х.
Определение. Арккосинусом числа хназывается такое число из отрезка 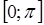 , косинус которого равен х.
, косинус которого равен х.
Определение. Арктангенсом числа хназывается такое число из интервала 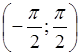 , тангенс которого равен х.
, тангенс которого равен х.
Определение. Арккотангенсом числа хназывается такое число из интервала 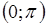 , котангенс которого равен х.
, котангенс которого равен х.
Арксинус, арккосинус, арктангенс и арккотангенс числового аргумента х обладают следующими свойствами, которые применяются при решении тригонометрических уравнений и неравенств:
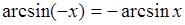
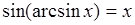 , где
, где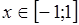
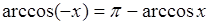
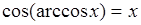 ,где
,где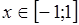
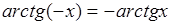
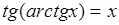 , где
, где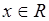
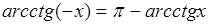
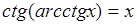 , где
, где 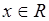
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|