Размещения с повторениями. Размещением из n по m c повторенияминазывается любой упорядоченный набор из m элементов выбранных случайным образом из генеральной совокупности, содержащей n элементов, если выбор производится с возвращением.. Перестановки с по

Размещения с повторениями

Размещением из n по m c повторенияминазывается любой упорядоченный набор из m элементов выбранных случайным образом из генеральной совокупности, содержащей n элементов, если выбор производится с возвращением.

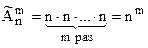число размещений с повторениями из n элементов по m (число вариантов такого упорядоченного выбора).

Объяснение: первый элемент можно выбрать n способами, второй – n и т.д. , а перемножаются они исходя из правила обобщённого умножения.

Перестановки с повторениями

Пусть имеются n элементов , причём среди них есть одинаковые ( 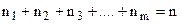, n_i –численности групп одинаковых элементов). Тогда число перестановок из этих элементов вычисляется по формуле:

Знаменатель указывает на то, что при перестановке одинаковых элементов между собой сама перестановка не меняется.

Разбиение на группы

Пусть имеются n элементов , их надо разбить на m групп так чтобы 1 группа содержала n1 элементов, вторая – n2 и т.д. ….m-я группа nm, причём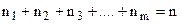

Тогда число способов осуществить это разбиение на группы рассчитывается по формуле:

Сочетания из 3 элементов по 2

(число неупорядоченных наборов из 3 элементов по 2 = 3)

(Общая формула )

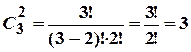
1).

Число способов осуществить указанный выбор

2).

⇐ Предыдущая 123 Следующая ⇒