
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ. при r>0 > при r<0. Формулы сокращённого умножения.
СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ
1. 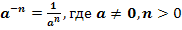
2. 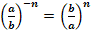
3. 
4.По определению: 
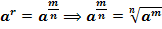
Свойства:
1. 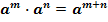
2. 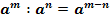
3. 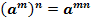
4. 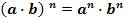
5. 
6. Пусть r рациональное число 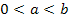 , тогда
, тогда
при r>0 > при r<0
7 .Для любого рациональных чисел r и s из неравенства 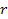 >
>  следует
следует
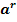 >
> 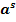 при a>1
при a>1 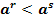 при
при 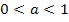
Формулы сокращённого умножения.
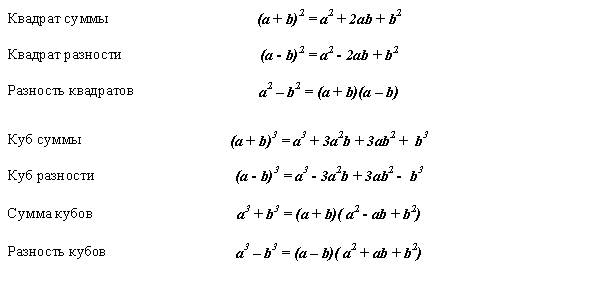
Пример 1. Упростите выражение 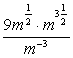 .
.
Решение
Применим свойства степеней (умножение степеней с одинаковым основанием и деление степеней с одинаковым основанием): 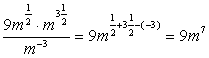 .
.
Ответ: 9m7 .
Пример 2.Сократить дробь: 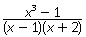
Решение.Так область определения дроби 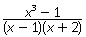 все числа, кроме х ≠ 1 и х ≠ -2.Вместе с тем
все числа, кроме х ≠ 1 и х ≠ -2.Вместе с тем  .Сократив дробь, получим
.Сократив дробь, получим 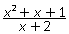 .Область определения полученной дроби: х ≠ -2, т.е. шире, чем область определения первоначальной дроби. Поэтому дроби
.Область определения полученной дроби: х ≠ -2, т.е. шире, чем область определения первоначальной дроби. Поэтому дроби 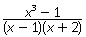 и
и 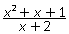 равны при х ≠ 1 и х ≠ -2.
равны при х ≠ 1 и х ≠ -2.
Пример 3.Сократить дробь: 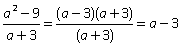
Пример 4.Упростить: 
Пример 5.Упростить: 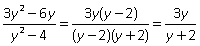
Пример 6. Упростить: 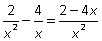
Пример 7. Упростить: 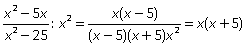
Пример 8.Упростить: 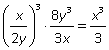
Пример 9. Вычислить: 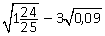 .
.
Решение. 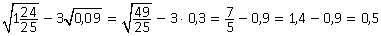
Пример 10.Упростить выражение: 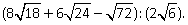
Решение. 
Пример 11.Сократить дробь 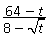 , если
, если 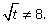
Решение. 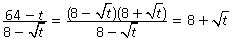 .
.
Пример 12.Освободиться от иррациональности в знаменателе дроби 
Решение. В знаменателе имеем иррациональность 2-й степени, поэтому помножим и числитель, и знаменатель дроби на сопряженное выражение, то есть сумму чисел 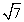 и
и 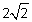 , тогда в знаменателе будем иметь разность квадратов, которая и ликвидирует иррациональность.
, тогда в знаменателе будем иметь разность квадратов, которая и ликвидирует иррациональность. 
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|