
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПРЕОБРАЗОВАНИЕ АЛГЕБРАИЧЕСКИХ, РАЦИОНАЛЬНЫХ, ИРРАЦИОНАЛЬНЫХ, СТЕПЕННЫХ ВЫРАЖЕНИЙ
ПРЕОБРАЗОВАНИЕ АЛГЕБРАИЧЕСКИХ, РАЦИОНАЛЬНЫХ, ИРРАЦИОНАЛЬНЫХ, СТЕПЕННЫХ ВЫРАЖЕНИЙ
Теоретические сведения.
КОРНИ НАТУРАЛЬНОЙ СТЕПЕНИ ИЗ ЧИСЛА, ИХ СВОЙСТВА.
Корень n – степени: 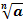 , n - показатель корня, а –подкоренное выражение
, n - показатель корня, а –подкоренное выражение
Если n – нечетное число, то выражение 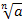 имеет смысл при
имеет смысл при 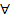 а
а
Если n – четное число, то выражение 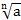 имеет смысл при
имеет смысл при 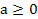
Арифметический корень: 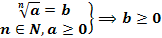
Корень нечетной степени из отрицательного числа: 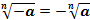
ОСНОВНЫЕ СВОЙСТВА КОРНЕЙ
1. Правило извлечения корня из произведения:
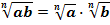
2.Правило извлечения корня из дроби:
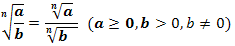
3. Правило извлечения корня из корня:
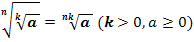
4. Правило вынесения множителя из под знака корня:
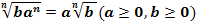
5. Внесение множителя под знак корня:
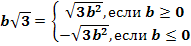 ,
,
6. Показатель корня и показатель подкоренного выражения можно умножить на одно и тоже число.
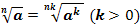
7. Правило возведения корня в степень.
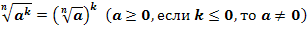
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
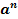 =
= 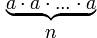 ,a – основание степени, n – показатель степени
,a – основание степени, n – показатель степени
Свойства:
1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остается неизменным.
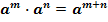
2. При делении степеней с одинаковыми основаниями показатели вычитаются, а основание остается неизменным.
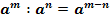
3. При возведении степени в степень показатели перемножаются.
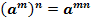
4. При возведении в степень произведения двух чисел, каждое число возводят в эту степень, а результаты перемножают.
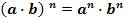
5. Если в степень возводят частное двух чисел, то в эту степень возводят числитель и знаменатель, а результат делят друг на друга.
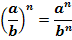
6. Если 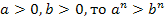
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|