
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Преобразование выражений, содержащих радикалы (урок 1)
Преобразование выражений, содержащих радикалы (урок 1)
На данном уроке мы рассмотрим преобразование выражений, содержащих радикалы, и прежде всего вынесение множителя за знак радикала и внесение множителя под знак радикала.
1. Повторение определений и свойств
Напомним основные определения.
Определение:
Корнем n-й степени из неотрицательного числа а называется такое неотрицательное число b, которое при возведении в степень n дает число а.
Приведем математическую запись определения:
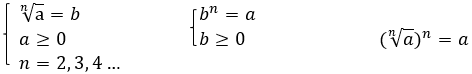
Например: 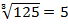 , т. к.
, т. к. 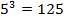 ;
; 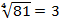 , т. к.
, т. к. 
Итак, в рассмотренном случае под корнем стоит строго неотрицательное число, но существует также корень из отрицательного числа – это корень нечетной степени, он существует для любых чисел.

Например: 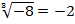 , т.к.
, т.к. 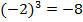 ,
, 
Напомним свойства корней n-й степени, которыми мы будем пользоваться при всех преобразованиях:
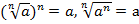 при
при 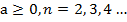
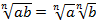 , при
, при  (теорема 1);
(теорема 1);
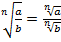 , при
, при 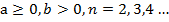 (теорема 2);
(теорема 2);
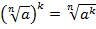 , при
, при 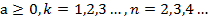 (теорема 3);
(теорема 3);
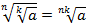 , при
, при  (теорема 4);
(теорема 4);
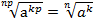 при
при 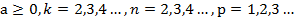 (теорема 5).
(теорема 5).
Все дальнейшие преобразования и вычисления базируются на определении и свойствах корня n-й степени.
Пример 1 – вычислить:
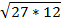
Разложим подкоренное выражение на более удобные множители и после этого извлечем корень:
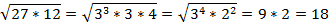
Пример 2 – упростить выражение:
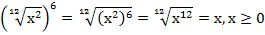
Пример 3 – упростить выражение:

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|