
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 2.
Задача 2.
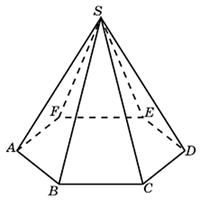
Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в двенадцать раз?
объем пирамиды равен одной трети произведения площади основания и высоты:
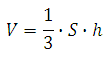
S – площадь основания
h – высота пирамиды
При увеличении высоты в 12 раз, объем пирамиды также увеличится в 12 раз (это прямолинейная зависимость):
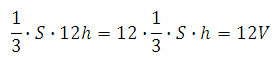
Ответ: 12
Задача 3.
Во сколько раз увеличится площадь поверхности правильного тетраэдра, если рёбра тетраэдра увеличить в 5 раз
Известно, что при увеличении (уменьшении) линейных размеров фигуры в k раз получается подобная ей фигура, их площади относятся как квадрат коэффициента подобия, то есть:

k – это есть коэффициент подобия
В данной задаче k=5.
То есть, с использованием свойства подобия задача решается устно:
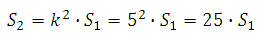
это означает, что площадь поверхности всей пирамиды также увеличится в 25 раз.
Ответ: 25
Задача 4. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
 Октаэдр это многогранник с восьмью граниями, все гарани это правильные треугольники.
Октаэдр это многогранник с восьмью граниями, все гарани это правильные треугольники.
При увеличении рёбер в три раза каждая грань полученного октаэдра будет подобна соответствующей ей грани исходного. Площадь каждай грани увеличится в 32 раз, то есть в 9 раз. Значит и площадь всей поверхности также увеличится в 9 раз.
|
2. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в 5 раз?
3. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если рёбра тетраэдра увеличить в 6 раз?
4. Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 4 раза?
5.Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 2 раза?
6. Во сколько раз увеличится объем октаэдра, если все его ребра увеличить в 4 раза?
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|