
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
случай кратных комплексных корней характеричтического уравнения (возможен только при
4. случай кратных комплексных корней характеричтического уравнения (возможен только при
Пусть 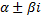 – корни кратности
– корни кратности 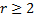 ,
, 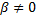 . Им соответствуют
. Им соответствуют 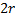 линейно независимых решений:
линейно независимых решений:
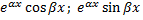
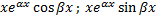
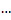
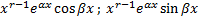 .
.
Теорема о структуре общего решения неоднородного ЛДУ n-го порядка. Теорема о наложении частных решений.

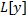 – линейный дифференциальный оператор с переменными коэффициентами
– линейный дифференциальный оператор с переменными коэффициентами 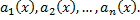
Теорема (о структуре общего решения неоднородного ЛДУ n-го порядка).
Пусть 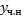 – частное решение ЛНДУ
– частное решение ЛНДУ 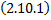 . Тогда
. Тогда 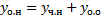
Док-во: нужно доказать, что 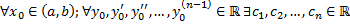 такие, что функция
такие, что функция 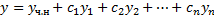 – решение ЛНДУ, удовлетворяющее начальным условиям
– решение ЛНДУ, удовлетворяющее начальным условиям
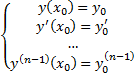 .
.
Решение задачи Коши существует и определено на 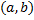 в силу теоремы существования. Рассмотрим разность
в силу теоремы существования. Рассмотрим разность 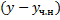 :
:
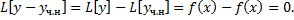
Т.е. 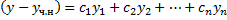 – решение ЛОДУ;
– решение ЛОДУ; 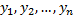 – ФСР ЛОДУ;
– ФСР ЛОДУ; 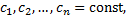
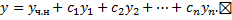
Теорема (о наложении частных решений).
Пусть 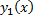 – частное решение ЛНДУ;
– частное решение ЛНДУ; 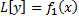 ;
; 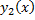 – частное решение ЛНДУ;
– частное решение ЛНДУ; 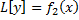 . Тогда
. Тогда 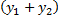 – частное решение ЛНДУ
– частное решение ЛНДУ 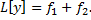
Док-во: 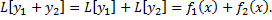
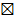
Нахождение частных решений неоднородного ЛДУ с постоянными коэффициентами и правой частью специального вида.
Пусть 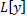 – линейный дифференциальный оператор с постоянными коэффициентами. Рассмотрим ЛНДУ:
– линейный дифференциальный оператор с постоянными коэффициентами. Рассмотрим ЛНДУ:

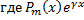 – квазимногочлен;
– квазимногочлен;
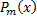 – многочлен степени
– многочлен степени 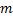 ;
;
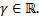
Тогда 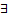 частное решение ЛНДУ (2.12.1) вида
частное решение ЛНДУ (2.12.1) вида
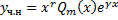 ,
,
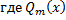 – многочлен степени
– многочлен степени 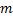 ;
; 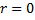 , если
, если 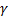 не является корнем характеристического уравнения соответствующего ЛОДУ; если
не является корнем характеристического уравнения соответствующего ЛОДУ; если 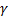 – корень, то
– корень, то 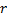 равен кратности корня
равен кратности корня 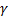 .
.
Замечание. Коэффициенты 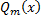 - неопределенные (заранее не известные), находятся методом неопределенных коэффициентов.
- неопределенные (заранее не известные), находятся методом неопределенных коэффициентов.
Пример 1.
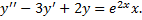
Соответствующее ЛОДУ: 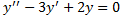 ,
,
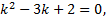
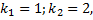
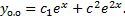
Найдем 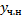 .
.
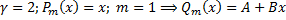 ;
;
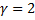 – корень характеристического уравнения ЛОДУ кратности
– корень характеристического уравнения ЛОДУ кратности 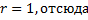
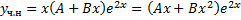 ,
,
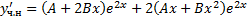 ,
,
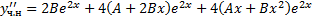 ,
,
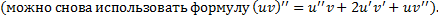
Чтобы найти 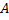 и
и 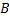 , подставим функцию в ЛНДУ:
, подставим функцию в ЛНДУ:
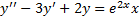 ,
,
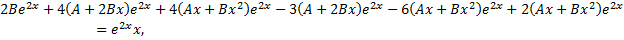
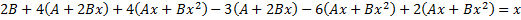 ,
,
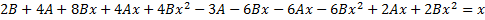 ,
,
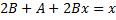 .
.
Коэффициент при 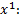 2
2 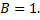
Коэффициент при 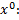
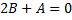 .
.
Получаем СЛАУ относительно 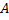 и
и 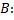
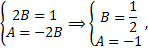
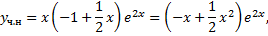
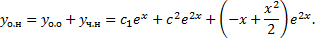
Рассмотрим ЛНДУ с постоянными коэффициентами
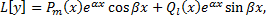
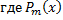 – многочлен степени
– многочлен степени 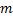 ;
;
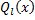 – многочлен степени
– многочлен степени 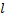 ;
;
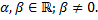
Тогда 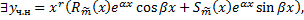
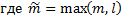 ;
; 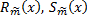 – многочлены степени
– многочлены степени 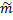 ;
;
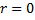 , если
, если 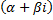 не является корнем характеристического уравнения соответствующего ЛОДУ;
не является корнем характеристического уравнения соответствующего ЛОДУ; 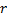 равен кратности корня, если
равен кратности корня, если 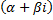 является корнем.
является корнем.
Пример 1.
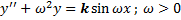
(уравнение колебаний при наличии внешней периодической силы частоты 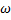 ).
).
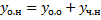 .
.
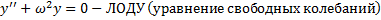 ,
,
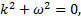
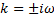 ,
,
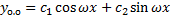 ,
,
.
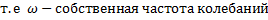 .
.
Найдем 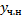 .
.
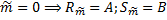 ,
,
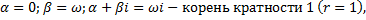
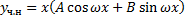
(частота внешней силы равна собственной частоте 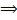 резонанс, амплитуда колебаний неограниченно возрастает).
резонанс, амплитуда колебаний неограниченно возрастает).
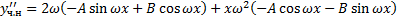
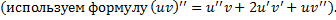
Чтобы найти 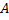 и
и 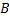 , подставим
, подставим 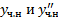 в ЛНДУ:
в ЛНДУ:
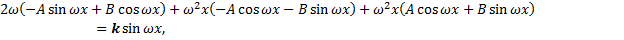
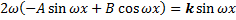 .
.
Коэффициент при 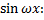
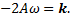
Коэффициент при 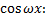
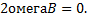
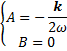
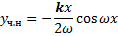
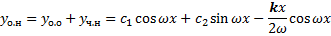
Пример 2.
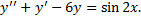
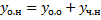 ,
,
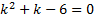 ,
,
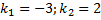 ,
,
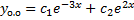 ,
,
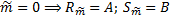 ,
,
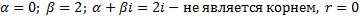 ,
,
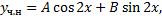
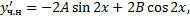
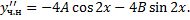
Чтобы найти 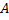 и
и 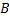 , подствим в ЛНДУ:
, подствим в ЛНДУ:
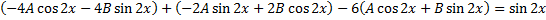
Коэффициент при 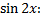
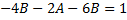 .
.
Коэффициент при 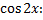
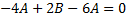 .
.
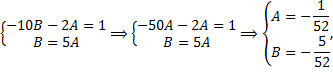
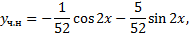
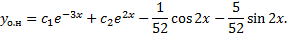
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|