
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Первое достаточное условие существования экстремума функции.
Первое достаточное условие существования экстремума функции.
Если при переходе через критическую точку 1 рода х=х0 производная функции 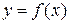 меняет знак, то х=хо- точка экстремума.
меняет знак, то х=хо- точка экстремума.
При этом если производная меняет знак с плюса на минус, то х=х0- точка максимума, а 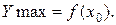
Если же производная меняет знак с минуса на плюс, то х=х0-точка минимума, а 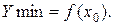
Второе достаточное условие существования экстремума функции.
Если в точке х=х0 первая производная функции 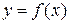 обращается в нуль, а вторая производная отлична от нуля, то х=х0- точка экстремума.
обращается в нуль, а вторая производная отлична от нуля, то х=х0- точка экстремума.
При этом если вторая производная в этой точке положительна 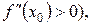 то х=х0-точка минимума; если вторая производная в этой точке отрицательна
то х=х0-точка минимума; если вторая производная в этой точке отрицательна 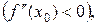 то х=х0- точка максимума.
то х=х0- точка максимума.
Ход работы
1. Решить две задачи с полным объяснением согласно варианта.
2. Ответить на вопросы самопроверки.
Варианты заданий
Задача № 1. Число 25 запишите в виде произведения двух положительных чисел, сумма которых наименьшая.
Задача № 2. Тело движется прямолинейно по закону 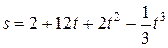 . Найдите максимальную скорость движения тела.
. Найдите максимальную скорость движения тела.
Задача № 3. Какие размеры должен иметь цилиндр, площадь полной поверхности которого 96p см2, чтобы его объём был наибольшим?
Задача № 4. Докажите, что из всех прямоугольников, имеющих периметр 32 см, наибольшую площадь имеет квадрат.
Задача № 5. Число 50 представьте в виде суммы двух положительных слагаемых так, чтобы произведение этих чисел было наибольшим.
Задача № 6. Какой из цилиндров с объёмом 128p см3 имеет наименьшую полную поверхность?
Задача № 7. Требуется изготовить ящик с крышкой, объём которого равен 288 см3, а стороны основания относятся как 1:3. Каковы должны быть размеры ящика, чтобы его полная поверхность была наименьшей?
Задача № 8. Около стены нужно сделать забор, чтобы огородить прямоугольный участок земли наибольшей площади. Общая длина забора 60 м. Найдите длину части забора, параллельной стене.
Задача № 9. Гипотенуза прямоугольного треугольника равна 8 см. Найдите длину каждого катета, если площадь треугольника должна быть наибольшей.
Задача № 10.Докажите, что из всех прямоугольников с площадью 400 см2 квадрат имеет наименьший периметр.
Задача № 11. Из всех прямоугольных параллелепипедов, у которых в основании лежит квадрат и площадь полной поверхности равна 600 см2, найдите параллелепипед наибольшего объёма и определите его размеры
Задача № 12Какое положительное число, будучи сложеное с обратным ему числом, даёт наименьшую сумму?
Задача № 13 Каковы должны быть размеры цилиндрического сосуда ёмкостью 8p литров, открытого сверху, чтоб на его изготовление потребовалось наименьшее количество материала.
Задача № 14 Из квадратного листа жести, сторона которого равна 30 см, нужно вырезать по углам четыре равных квадрата так, чтобы из оставшейся части после сгибания получить коробку наибольшей ёмкости. Каковы при этом размеры вырезанных квадратов?
Задача № 15Тело движется прямолинейно по закону: 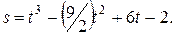 Найдите минимальную скорость движения тела.
Найдите минимальную скорость движения тела.
Задача № 16 Из куска проволоки длиной 40 см согнут прямоугольник наибольшей площади. Каковы размеры этого прямоугольника?
Задача № 17Тело движется прямолинейно по закону 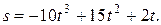 Найдите максимальную скорость движения тела.
Найдите максимальную скорость движения тела.
Задача № 18Разложите число 8 на два слагаемых так, чтобы сумма их кубов была наибольшей.
Задача № 19Прямолинейное движение точки задано уравнением: 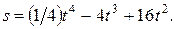 В какие моменты времени скорость движения точки равна нулю ?
В какие моменты времени скорость движения точки равна нулю ?
Задача № 20Сумма основания и высоты треугольника равна 24 см. Каковы должны быть размеры основания, чтобы площадь треугольника была наибольшей
Задача № 21 Точка движется по прямой по закону: 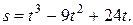 Найдите скорость и ускорение движения. В какие моменты времени точка меняет направление движения?
Найдите скорость и ускорение движения. В какие моменты времени точка меняет направление движения?
Задача № 22 Из листа картона прямоугольной формы размером 30х50 см2нужно вырезать по углам квадраты так, чтобы из оставшейся части после сгибания получить коробку наибольшей боковой поверхности. Каковы при этом размеры вырезанных квадратов?
Задача № 23 Разложите число 10 на два слагаемых так, чтобы сумма их квадратов была наименьшей.
Задача № 24 Точка движется прямолинейно по закону: 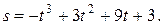 Найдите максимальную скорость движения тела.
Найдите максимальную скорость движения тела.
Задача № 25 Требуется изготовить ящик с крышкой, объём которого равен 72 см3, стороны основания относятся, как 1:2. Каковы должны быть размеры ящика, чтобы его полная поверхность была наименьшей?
Задача № 26 Одна сторона прямоугольного участка земли примыкает к берегу канала, а три другие огораживаются забором. Каковы должны быть размеры этого участка, чтобы его площадь равнялась 800 м2, а длина забора была наименьшей?
Задача № 27 Резервуар ёмкостью 4м3 квадратным основанием, открытый сверху, нужно выложить оловом. Каковы должны быть размеры резервуара, чтобы израсходовать наименьшее количество олова?
Задача № 28Прямолинейное движение точки задано уравнением: 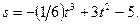 Найдите скорость движения точки в тот момент, когда ускорение равно нулю ?
Найдите скорость движения точки в тот момент, когда ускорение равно нулю ?
Вопросы для самопроверки
1. В чем состоит физический смысл производной?
2. В чем состоит физический смысл второй производной?
3. Как найти промежутки возрастания и убывания функции?
4. Как найти точки экстремума функции и значение функции в точках экстремума?
5. Составьте уравнение касательной к кривой у = х2 - 4х в точке с абсциссой х = 1
Использованная литература
1. В.В. Пак, Ю.Л. Носенко «Высшая математика» К, «Лебедь», 1996
2. Н.В. Богомолов «Практические занятия по математике» М. «Высшая школа», 1979
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|