Инструкционная карта. Теоретическое обоснование работы. Приложения производной к исследованию функций.

Инструкционная карта

практического занятия № 10

по учебной дисциплинеЕН.01 Математика

Специальности:

21.02.15 «Открытые горные работы»

13.02.11 «Техническая эксплуатация и обслуживание электрического и электро-механического оборудования (горная промышленность)»

23.02.01 «Организация перевозок и управление на транспорте (автомобильном)»

Тема занятия: Использование производной для решения оптимизационных задач.

Тип занятия: практическое.

Цель занятия:

Дидактическая: Овладеть методикой решения оптимизационных задач с помощью производной.

Воспитательная: Воспитать у студентов настойчивость в достижении цели, чувство ответственности в овладении знаниями, нужными в будущей профессиональной деятельности.

Междисциплинарная интеграция: ОДП.01 «Математика», ОДП.02 «Физика».

Методическое обеспечение: инструкционные карты, опорные конспекты по использованию производной для решения прикладных задач.

Теоретическое обоснование работы

Приложения производной к исследованию функций.

Дифференцируемая функция 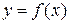возрастает на промежутке 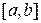, если её производная положительна в каждой точке этого промежутка.

Дифференцируемая функция 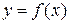убывает в промежутке 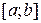, если её производная отрицательна в каждой точке этого промежутка.

Функция 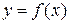имеет максимум в точке х=х_1, если для всех значений х, достаточно близких к х₁, выполняется неравенство 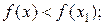х=х₁-точка максимума; - максимум функции.

Функция 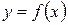имеет минимум в точке х=х₂ если для всех значений х, достаточно близких к х_2,выполняется неравенство 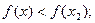х=х₂-точка минимума; 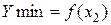- минимум функции.

Точки максимума и минимума называются точками экстремума,а значения функции в этих точках –экстремальными.

Точки, в которых производная функция обращается в ноль, называются критическими точками 1 рода.

12 Следующая ⇒