Практика 4. Линейное преобразование сигналов. научиться создавать сигналы сложной формы, используя свойства линейности;. познакомиться с методами разложения сигнала в гармонический ряд Фурье.. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Стр 1 из 2Следующая ⇒

Практика 4

Линейное преобразование сигналов

Цель работы:

1) научиться создавать сигналы сложной формы, используя свойства линейности;

2) познакомиться с методами разложения сигнала в гармонический ряд Фурье.

Руководство по лабораторной работе: для выполнения лабораторной работы Вам необходимо повторить лекционный материал:

– 2.3 Спектры периодических сигналов

– 2.4 Преобразование Фурье

Скачать материал к лабораторной работе №4: basic-dsp-Lab4.zip

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Формирование сложных последовательностей сигналов можно осуществлять с помощью линейных математических операций – умножения на константу, сложения и временного сдвига. В качестве примера рассмотрим формирование последовательности прямоугольных импульсов из соответствующих гармонических составляющих.

Формула, описывающая разложение импульсного периодического сигнала на гармонические составляющие выглядит следующим образом:

Программа, реализующая эту функцию для восьми гармонических составляющих, выглядит следующим образом (пример № 1):

N=8; %число ненулевых гармоник
t = -1:0.01:1; %вектор моментов времени
A = 1; %амплитуда
T = 1; %период
nh = (1:N)*2 – 1; %номера ненулевых гармоник
% вычисление строк-гармоник
harmonics = cos(2*pi*nh’*t/T);
Am = 2/pi./nh; %амплитуды гармоник
Am(2:2:end)=-Am(2:2:end); %чередование знаков
s1 = harmonics.*repmat(Am’, 1, length(t));
%формирование строк – частных сумм гармоник
s2 = cumsum(s1);
for k=1:N,
subplot(4,2,k); plot(t,s2(k,:))
end

Результат работы данной программы показан на рисунке 1.

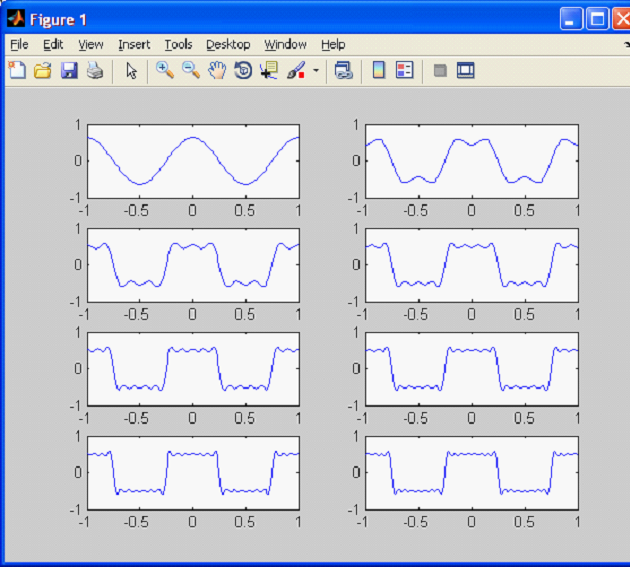
Рисунок 1. Формирование импульсного сигнала из восьми гармонических составляющих.

Для полного понимания принципа работы программы – посмотрите документацию для следующих функций – repmatи cumsum.

Генерировать периодические сигналы различной формы можно с помощью встроенных функций среды MatLab:
square –последовательность прямоугольных импульсов;
sawtooth –последовательность треугольных импульсов;
diric –функция Дирихле (периодическая sinc-функция);
chirp –генерация колебаний с меняющейся частотой.

Для генерации дискретного белого шума с нормальным распределением можно использовать функцию randn(m, n).В результате вызова этой функции генерируется массив, содержащий mстрок и n столбцов псевдослучайных чисел, имеющих нормальное распределение с нулевым математическим ожиданием и единичной дисперсией. Пример работы этой функции показан ниже:

12 Следующая ⇒