Сложение вероятностей.Событие А В наступает, если наступают оба события А и В одновременно. Пусть А и В — два события одного случайного опыта. Рассмотрим те элементарные события, которые благоприятствуют событию А, и те элементарные события, которые благ

Сложение вероятностей.Событие А В наступает, если наступают оба события А и В одновременно. Пусть А и В — два события одного случайного опыта. Рассмотрим те элементарные события, которые благоприятствуют событию А, и те элементарные события, которые благоприятствуют событию В. Все вместе эти элементарные события благоприятствуют новому событию, которое называется объединением событий А и В. Событие А В наступает, если наступает хотя бы одно из событий А или В. Это означает, что наступает либо А, либо В, либо А и В вместе. Пусть А и В — два события одного случайного опыта. Рассмотрим элементарные события, которые благоприятствуют и событию А и событию В. Все вместе эти элементарные события благоприятствуют новому событию, которое называется пересечением событий Аи В. Если события А и В не имеют общих благоприятствующих элементарных событий, то они не могут наступить одновременно в ходе одного и того же опыта (еще говорят взаимоисключающие). Такие события называют несовместными, а их пересечение — пустое событие. Если события А и В несовместны, то Р(А В) = Р(А) + Р (В)Б) Если А и В — любые события, то Р(А В) = Р(А) + Р (В) - Р(А В)

Случайный выбор — это выбор наудачу одного предмета из группы предметов. Выбор наудачу — это разновидность случайного опыта с равновозможными элементарными событиями. Элементарным событием в таком опыте является извлечение одного предмета из группы. Если в группе N предметов, то каждый из них может быть выбран с вероятностью 1/N. После выбора одного предмета случайный выбор можно продолжить, выбрав второй, третий и т. д. предметы или сразу взять наудачу нужное количество предметов. Собранную таким образом группу называют случайной выборкой. Независимые события — это события, которые не связаны друг с другом, т.е. по наступлению одного из них нельзя судить о вероятности другого. Например, при бросании двух костей результат бросания первой кости не влияет на результат бросания второй. Если события А и В независимы, то Р(А 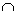В) = Р(А) · Р(В).

Критерии оценки

Если практическая работа выполнена в полном объеме и правильно оформлена, то ставится оценка «5».Если практическая работа выполнена более чем на 80-89%, ставится оценка «4». Если практическая работа выполнена более чем на 70-79 %, ставится оценка «3». В противном случае работа не засчитывается.

⇐ Предыдущая 12