Задача 2.

Ребята, предлагаю Вам проработать тему «Сумма углов треугольника»

Блез Паскаль, великий французский учёный 17-го века, заметил, что у всех треугольников сумма 3-х углов равна 180 градусов. И у него возник вопрос: «Как это доказать?»

И он отрезал ножницами два уголка треугольника и приложил их к третьему углу. В результате получился развёрнутый угол, градусная мера которого, как вам уже известно, равна 180 градусов.

Теорема:

Сумма углов треугольника равна 180 градусов.

Доказательство:

Пусть АВС - произвольный треугольник. Доказать, что ∠А+∠В+∠С= 180 градусов.

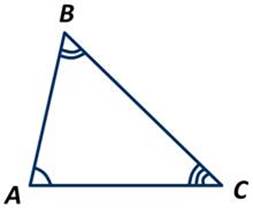
Проведём прямую а через точку В параллельно стороне АС.

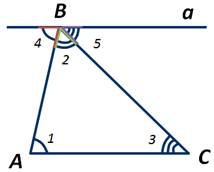
∠1 и ∠4 - внутренние накрест лежащие углы при параллельных прямых а и АС и секущей АВ. А значит, ∠1=∠4. ∠3 и ∠5 являются внутренними накрест лежащими при параллельных прямых а и АС и секущей ВС. Следовательно, ∠3=∠5.

Сумма градусных мер ∠4, ∠2 и ∠5 равна градусной мере развёрнутого угла с вершиной в точке В, то есть ∠4+∠2+∠5=180 градусов.

А так как ∠1=∠4, ∠3=∠5, то получаем, что ∠1+∠2+∠3=180 градусов. То есть ∠А+∠В+∠С=180 градусов. Теорема доказана.

Внешним углом треугольника называют угол, смежный с каким-либо углом треугольника.

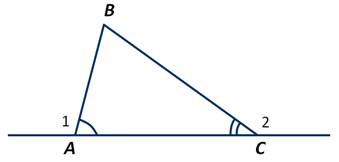
Например, ∠1 - внешний угол треугольника АВС, смежный с ∠ВАС. ∠2 - внешний угол, смежный с ∠АСВ.

Теорема:

Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.

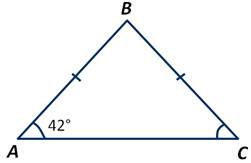Задача 1

Дано: ∆АВС, АВ=ВС, ∠А=42⁰.

Найти: ∠В?

Решение

Так как АВ=ВС, то треугольник АВС является равнобедренным. По свойству равнобедренного треугольника ∠А=∠С=42⁰.

По теореме о сумме углов треугольника ∠А+∠В+∠С=180 градусов. Значит,

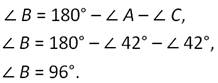
Ответ: 42⁰.

Задача 2.

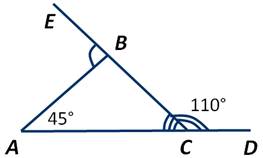
Дано: ∆АВС. ∠ВСD=110⁰, ∠ВАС=45⁰ Найти ∠АВЕ.

Решение

∠ВСD и ∠ВСА – смежные. По теореме о сумме смежных углов:

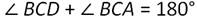
Тогда:

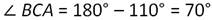
∠АВЕ является внешним углом нашего треугольника, смежным с ∠АВС. По теореме о внешнем угле:

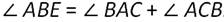
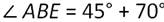
∠АВЕ=115⁰.

Ответ: 115⁰

Задача 3

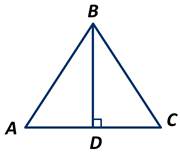∆АВС – равнобедренный; ВD - высота. ∠АВС=56⁰

Найдите градусные меры углов треугольника ABD.

Решение

По условию треугольник АВС - равнобедренный, то высота ВD, проведённая к основанию, является также и биссектрисой. Значит:

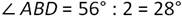
∠АDВ=90⁰, так как ВD - высота.

По теореме о сумме углов треугольника, получаем:

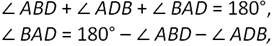
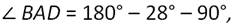
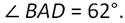
Ответ: ∠АDВ=90⁰, ∠ВАD=62⁰, ∠ABD=28⁰.

12 Следующая ⇒