
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
The section matrix
2.2.3 The section matrix
Topological matrixes can be compiled for graph sections too.
The section matrix 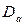 , corresponding to the directed graph with “
, corresponding to the directed graph with “ 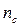 ” sections and “
” sections and “ 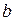 ” branches is the name for the matrix
” branches is the name for the matrix 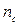

 .
.
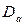 =
= 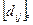 (2.11)
(2.11)
where 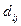 is an element of the matrix
is an element of the matrix 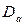 ,
, 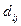 =1, if the branch
=1, if the branch 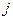 is incident to the section
is incident to the section 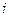 and coincides with the direction of the section;
and coincides with the direction of the section; 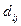 =-1, if the branch
=-1, if the branch 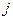 is incident to the section
is incident to the section 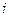 and opposite to the direction of the section;
and opposite to the direction of the section; 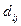 =0, if the branch
=0, if the branch 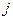 is not incident to the section
is not incident to the section 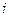 . For instance, for the directed graph in Fig. 2.2,c it is possible to choose 7 sections:
. For instance, for the directed graph in Fig. 2.2,c it is possible to choose 7 sections: 
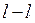 ,
,  ,
,  ,
, 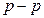 ,
,  ,
,
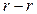 .
.
Section directions are marked with arrows on section lines. As a result, we get a section matrix
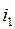
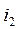
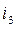
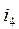

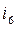
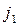
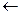 branches
branches
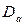 =
= 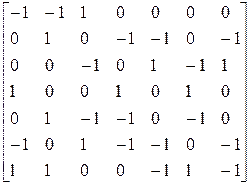
 (2.12)
(2.12)
sections
It is obvious, that some sections used in the matrix (2.12) are linearly dependent. Only a section that includes at least one branch not being part of any other section is considered to be linearly independent. The number of independent sections, evidently, is equal to the number of independent nodes. Therefore, it is possible to retain any three lines in the matrix (2.12) without losing any information. So, having excluded the first four lines, we get the matrix:
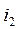
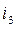
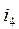

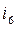
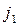
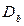 =
= 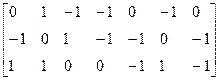
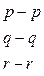 (2.13)
(2.13)
The matrix 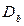 is called the base section matrix. The use of the tree
is called the base section matrix. The use of the tree  pre-supposes use the systematic method of construction of the base section matrix, that is, the base matrix is to correspond to the graph main sections. Such a matrix is called the main section matrix
pre-supposes use the systematic method of construction of the base section matrix, that is, the base matrix is to correspond to the graph main sections. Such a matrix is called the main section matrix 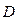 . Directions of main sections are taken according to the direction of the corresponding edges of the graph tree. So, having arranged the edges in the lower columns we get the matrix
. Directions of main sections are taken according to the direction of the corresponding edges of the graph tree. So, having arranged the edges in the lower columns we get the matrix 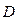 :
:
edges the rest of graph branches
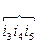
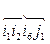
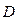 =
= 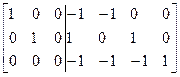
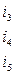 (2.14)
(2.14)
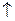
edges
One can see from (2.14) that any matrix 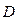 can be divided in the following way:
can be divided in the following way:
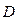 =
= 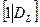 (2.15)
(2.15)
where, the unit matrix 1 corresponds to the edges
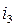
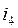

 edges
edges
1= 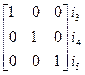 (2.16)
(2.16)
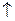
edges
The matrix 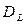 corresponds to the rest of graph branches
corresponds to the rest of graph branches
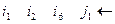 the rest of graph branches
the rest of graph branches
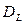 =
= 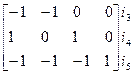 (2.17)
(2.17)
edges
So, as the unit matrix is in the matrix  , we can say that the lines of the matrix
, we can say that the lines of the matrix  are linearly independent.
are linearly independent.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|