The Principles of Circuit Topology

2. The Principles of Circuit Topology

2.1 Basic Topology Concepts

In circuit analysis, geometric representations of circuits, based on topology, are often used. Topology is the part of mathematics called graph theory. Topology studies the properties of geometric figures not dependant on these figure sizes.

The basic topology concepts are the following: branch, node, path, loop, graph, tree, edge, chord, and cross-section.

Fig. 2.1

A branch is a subcircuit carrying the same current. Graphically, it is represented by a line. Fig. 2.1 shows an electric circuit diagram. The subcircuits with the resistances 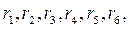the EMF 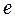, and the current source 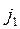are branches, i.e. each subcircuit carries the same current 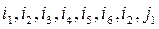, respectively.

A node is a place where branches are connected. Graphically, it is represented by a point. In Fig. 2.1 points 1 - 4.A are the nodes. An eliminable node is the place where two branches connect because the common branches carry the same current and they can be replaced by one branch. The point A in Fig. 2.1 is the eliminable node because the voltage source 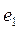and resistance 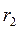carry the same current 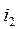and these elements can be represented by one branch. All the nodes of the diagram, except one, are called independent.

A path is a set of branches connecting two nodes without branching. In Fig. 2.1 the branches 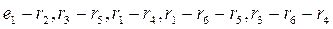make paths between the nodes 1 and 2. The branches 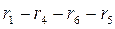do not make a path, because they have a branching in the section .

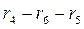A loop is a closed path encompassing several branches. In Fig. 2.1 the branches

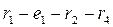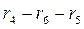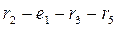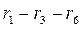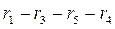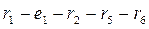. . . . . . make loops. An eliminable loop is a loop that includes a branch with an ideal current source, because the internal resistance of an ideal current source is infinitely great so in terms of resistance, the branch with an ideal current source is equivalent to a break. In addition, the current of an ideal current source is a known and unchanged value. In Fig. 2.1, the loop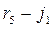

is eliminable.

Fig. 2.2

A graph is a geometric representation of an electric circuit in which all circuit branches are replaced by lines, and nodes are replaced by points. Fig. 2.2 shows a graph of the electric circuit in Fig. 2.1. Here the eliminable node A is excluded and the elements 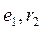make one branch of the graph. The other branches are designated as 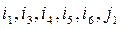. The connected graph is a graph that has a path between any two nodes. The graph in Fig. 2.2 is a circuit-connected graph. Excluding some graph branches produces a subgraph. The subgraph in Fig. 2.2 is represented as a graph produced by excluding, for example, branches 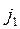and, thus, including only branches .

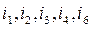A graph tree is a subgraph of a circuit-connected graph that includes all graph nodes but contains no loop. Some graph trees of the graph in Fig. 2.2 are shown in Fig. 2.3 (full lines). Apparently, it is possible to build several trees for the given graph, because it is possible to connect graph nodes in different ways. However, a graph tree can not include branches with an ideal current source for the reason indicated earlier, i.e. when building a graph tree, any ideal current source is replaced by a break. Thus, the number of graph tree branches is one less than the number of nodes, that is, it equals the number of independent graph nodes.

An edge is a branch of a graph tree. In Fig. 2.3,a the branches 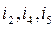are edges. In Fig. 2.3,b the branches 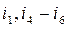are defined as edges. In Fig. 2.3,b the branches 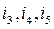are edges.

A subgraph is called a complementary to a tree when it complements a tree to a graph. Some tree complements (dotted lines) are shown in Fig. 2.3

A chord is a branch that does not belong to a tree. In Fig. 2.3,a the branches 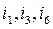are chords of the tree made by the branches 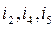; in Fig. 2.3,b the branches 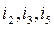are the chords of the tree made by the branches ;

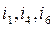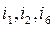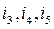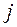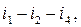
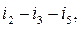
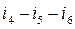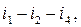
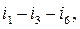
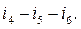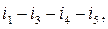
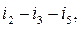
In Fig. 2.3,b branches are the chords of the tree made by the branches . A branch made by ideal the ideal current source cannot be a chord. A loop is made by adding a chord to a tree. Such a loop is the main loop or an independent loop. In Fig. 2.3,a the main loops are . In Fig. 2.3,b the main loops are In Fig.2.3,c the main loops are 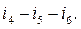The number of main loops equals the number of graph tree chords.

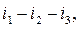
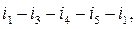
A cross-section is a set of circuit-connected graph branches, the elimination of which (but not the endings of the branch set) makes a graph which is not a circuit connected one. In order to obtain a cross – section we use a section line (or surface), while none of the branches is crossed twice. A line or a surface of section divides a graph into two parts. Fig.2.3,a shows the sections obtained by means of the lines of section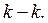

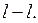
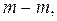respectively. Sections that include only one edge of a selected tree are called main or independent sections. Proceeding from the above – mentioned sections, we can say that the sections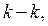 are the main ones, i.e. the first of them includes only one edge 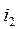, and the second – only one edge of the graph tree. The section 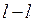is not a main one because it includes two edges 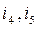of the graph tree. In Fig. 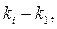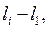2.3,b all sections 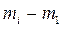are main ones, because each of them includes only one edge 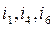of the graph tree, respectively.

12 3 4 Следующая ⇒