Хелпикс

Главная

Контакты

Случайная статья



Последовательность коэффициентов автокорреляции уровней временного ряда с возрастающими значениями лага называют функцией автокорреляционной.

⇐ ПредыдущаяСтр 2 из 2


Последовательность коэффициентов автокорреляции уровней временного ряда с возрастающими значениями лага называют функцией автокорреляционной.

Проверка значимости выборочного коэффициента парной линейной корреляции требует проверки статистической гипотезы: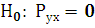

Пусть : У – признак-результат, Х1, Х2 – признаки – факторы. По исходным данным вычислены средние уровни признаков, средние квадратические отклонения значений признаков от средних уровней признаков

 ,у.=37,8; ,,х-1..=18,5;  ,,х-2..= 10,5

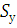=2,4; 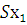   = 1,2;    𝑆,х-2.=0,8 и построено уравнение регрессии в стандартизированном масштабе 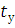=0,82 * ,𝑡-х1.+0,18∗,𝑡-х2.+ U Тогда теоретические (расчетные) значения признака – результата вычисляют по формуле : у(х)=1,79+1,64* 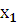+0,54*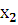

Пусть : У – признак-результат, Х1, Х2 – признаки – факторы. По исходным данным вычислены средние уровни признаков, средние квадратические отклонения значений признаков от средних уровней признаков

 ,у.=5,5; ,,х-1..=35,3;  ,,х-2..= 31,6

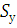=0,4; 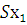   = 1,9;    𝑆,х-2.=1,6 преобразование уравнения «чистой» регрессии (уравнения регрессии в натуральном масштабе) к уравнению регрессии в стандартизованном масштабе выполняют по формулам:

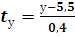  , ,𝒕-,х-𝟏..=,,х-𝟏.−𝟑𝟓,𝟑-𝟏,𝟗. , ,𝒕-,х-𝟐..=,,х-𝟐.−𝟑𝟏,𝟔-𝟏,𝟔.

Пусть : У – признак-результат, Х1, Х2 – признаки – факторы. По исходным данным вычислены средние уровни признаков, средние квадратические отклонения значений признаков от средних уровней признаков

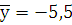; ,,х-1..=35,3;  ,,х-2..= - 31,6

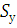=0,4; 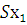   = 2,9;    𝑆,х-2.=2,6 преобразование уравнения «чистой» регрессии (уравнения регрессии в натуральном масштабе) к уравнению регрессии в стандартизованном масштабе выполняют по формулам:

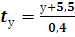  , ,𝒕-,х-𝟏..=,,х-𝟏.−𝟑��,𝟑-𝟐,𝟗. , ,𝒕-,х-𝟐..=,,х-𝟐.+𝟑𝟏,𝟔-𝟐,𝟔.

Пусть     ,𝑆𝑥-2.=36; 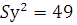 уравнение регрессии и выборочные дисперсии значений признаков Х и У соответственно. Тогда выборочный коэффициент парной линейной корреляции равен: 0,36

Пусть: n-количество наблюдений, m-число параметров при факторах уравнения множественной регрессии. Скорректированный индекс детерминации ( 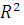скорр.) связан с индексом детерминации ,(𝑅-2 .) равенством:

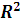скорр=1 – (1 - 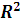) * ,(𝒏−𝟏)-(𝒏−𝒎−𝟏).

Пусть: при 5% - ом уровне значимости DW и DW1 – верхняя и нижняя границы критерия Дарбина – Уотсона; DW – фактическое значение критерия. Нулевая гипотеза об отсутствии автокорреляции в остатках отклоняется при условии: DW< DW1

 Пусть : У – признак-результат, Х1, Х2 – признаки – факторы. По исходным данным вычислены средние уровни признаков, средние квадратические отклонения значений признаков от средних уровней признаков:

 

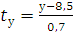  , ,𝑡-,х-1..=,,х-1.+3,3-0,9. , ,𝑡-,х-2..=,,х-2.−11,6-0,6.

Пусть : У – признак-результат, Х1, Х2 – признаки – факторы. По исходным данным вычислены средние уровни признаков, средние квадратические отклонения значений признаков от средних уровней признаков

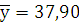; ,,х-1..=28,50;      ,,х-2..= 34,50

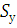=3,60;  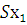  = 2,25;    𝑆,х-2.=1,80 и построено уравнение регрессии в стандартизированном масштабе 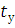= - 0,15 * ,𝑡-х1.+0,65∗,𝑡-х2.+ U Тогда теоретические (расчетные) значения признака – результата вычисляют по формуле : у(х)= - 0, 11 – 0,24* 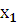+1,3*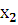

Пусть : У – признак-результат, Х1, Х2 – признаки – факторы. По исходным данным вычислены средние уровни признаков, средние квадратические отклонения значений признаков от средних уровней признаков

 ,у.=38,40; ,,х-1..=21,50;  ,,х-2..= 28,20

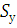=3,75;  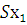  = 1,50;    𝑆,х-2.=1,65 и построено уравнение регрессии в стандартизированном масштабе 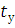= 0,96 * ,𝑡-х1.−0,22∗,𝑡-х2.+ U Тогда теоретические (расчетные) значения признака – результата вычисляют по формуле : у(х)= 0, 9 + 2,4*  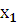– 0,5*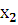

Пусть: при 5% - ом уровне значимости DW и DW1 – верхняя и нижняя границы критерия Дарбина – Уотсона; DW – фактическое значение критерия. Нулевая гипотеза об отсутствии автокорреляции в остатках не отклоняется при условии: DW > DW1

По данным, характеризующим некоторый объект за несколько последовательных моментов или периодов времени, можно построить: модели временного (динамического) ряда

По наблюдаемым значениям признака – результата Y и факторных признаков 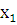,  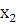,  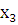вычислены значения величин: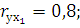

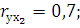
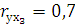
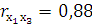
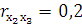    выберите правильное заключение: можно рекомендовать исключить из модели фактор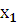  

По наблюдаемым значениям признака – результата Y и факторных признаков ,  ,  вычислены значения величин: . Выберите правильное заключение: Незначительное изменение исходных данных приведет к существенному изменению оценок параметров модели

По 25 – ти наблюдениям построено уравнение регрессии у ( 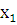)= 474 + 30* 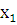+е. Коэффициент линейной корреляции составил 0,65. После включения в модель фактора  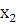индекс множественной корреляции составил 0,7. На уровне значимости 0,05 табличное значение F – критерия равно 4,3. Включение в эконометрическую модель фактора  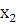незначимо, так как фактическое значение частного F – критерия равно: 2,9

 

Целесообразность включения факторов в модель регрессии можно оценить с помощью коэффициентов частной корреляции.

Фактическое значение критерия Стьюдента ( 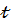 - критерия) для параметра  множественной линейной регрессии, вычисленного со стандартной ошибкой 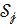, вычисляют по формуле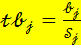   

Факторная (объясненная) сумма квадратов отклонений для регрессии вычисляется по формуле:

                                                                               

 


⇐ Предыдущая12
  

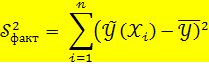
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.