Контакты

Случайная статья

Автокоррекция уровней временного ряда – это коррекционная связь между последовательными значениями УРОВНЕЙ РЯДА

Стр 1 из 2Следующая ⇒

Автокоррекция уровней временного ряда – это коррекционная связь между последовательными значениями УРОВНЕЙ РЯДА

В основе методов наименьших квадратов лежит минимализация выражения

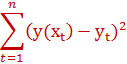
как функции параметров регрессии.

Вычислены частные коэффициенты линейной коррекции первого порядка:

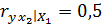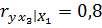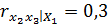; ; . Тогда частный коэффициент линейной коррекции второго порядка 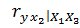равен 0,45; 1,14; 0,80.

Вычислены частные коэффициенты линейной коррекции первого порядка:

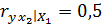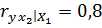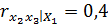; ; . Тогда частный коэффициент линейной коррекции второго порядка 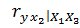равен 0,33.

Вычислены частные коэффициенты линейной коррекции первого порядка:

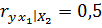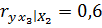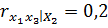; ; . Тогда частный коэффициент линейной коррекции второго порядка 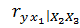равен 0,48.

Вычислены частные коэффициенты линейной коррекции первого порядка:

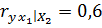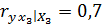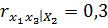; ; . Тогда частный коэффициент линейной коррекции второго порядка 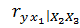равен 0,57.

Вычислены частные коэффициенты линейной коррекции первого порядка:

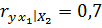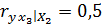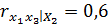; ; . Тогда частный коэффициент линейной коррекции второго порядка 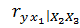равен 0,58.

Вычислены частные коэффициенты линейной коррекции первого порядка:

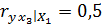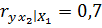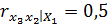; ; . Тогда частный коэффициент линейной коррекции второго порядка равен 0,24.

В случаи парной линейной регрессии факторная сумма квадратов отклонений имеет число степеней свободы, равное числу 1.

В уравнении регрессии 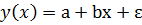величины a,b являются параметрами уравнения регрессии.

Если, выборочные средние квадратические отклонения значений результирующего признака 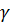и факторов признака 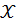от 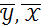равны 2, 4 и 1, 2 соответственно, то уравнением парной линейной регрессии может быть уравнение: = 3 1,4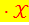

Если сумма квадратов отклонений значений признака – результата 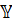от его среднего уровня равна 5, 7, а остаточная сумма квадратов отклонений для уравнения множественной регрессии равна 0,9, то степень тесноты связи признака 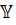с набором признаков – факторов, включенных в модель регрессии, можно оценить (с точностью 0,01) числом 0,92.

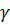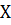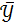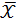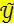
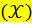
Если, выборочные средние квадратические отклонения значений результирующего признака и факторов признака и , равны 2, 4 и 1, 2 соответственно, то уравнением парной линейной регрессии может быть уравнение: - 3 + 1,4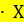

Если 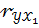= 0,8; 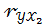= 0,6; 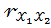=0,5, то стандартизованные коэффициенты регрессии (β – коэффициенты) являются решением системы уравнений:

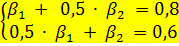
Если 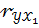= 0,8; 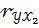= 0,9; 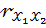= 0,3, то стандартизованные коэффициенты регрессии (β – коэффициенты) являются решением системы уравнений:

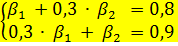
Если 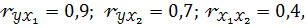то стандартизованные коэффициенты регрессии (β – коэффициенты) являются решением: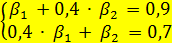

Если 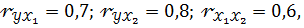то стандартизованные коэффициенты регрессии (β – коэффициенты) являются решением системы уравнений:

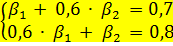
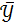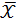Если = 3, = 2, 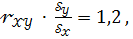то уравнение парной линейной регрессии имеет вид: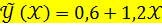

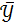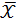Если = 3, = 2, 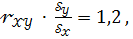то уравнение парной линейной регрессии

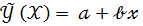равен 0,6

Если число коэффициентов эконометрической структурной модели равно числу коэффициентов соответствующей приведенной модели и структурные коэффициенты однозначно определяются по приведенным коэффициентам , то структурная модель называется идентифицируемой.

Если наблюдаются стабильные темпы роста показателя, то модель тенденции в динамике показателя можно выразить уравнением: =

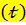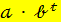
Если число коэффициентов экономической структурной модели больше числа коэффициентов соответствующей приведенной модели, то структурная модель называется частично идентифицируемой.

Если в течении продолжительного периода времени регулярно наблюдается смена роста и снижения уровней временного ряда через равные короткие промежутки времени, то модель уровня такого ряда включает периодические колебания.

Если в системе экономических уравнений каждая зависимая переменная рассматривается как явно заданная функция от данного набора факторов, то такую систему называют системой независимых уравнений.

Если значение выборочного коэффициента парной линейной корреляции близко к нулю, то можно предположить, что: значения признака – результата не изменяются с изменением значений факторного признака.

Если значение выборочного коэффициента парной линейной корреляции значимо и является отрицательным числом, то значения признака – результата убывают одновременно с ростом значений факторного признака.

Если функция регрессии нелинейная, то оценка значимости ее параметров производится для линеаризованной формы функции.

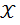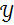Если значение критической точки, найденное по таблице «Критические точки распределения Стьюдента», равно 1,78, то нулевая гипотеза об отсутствии линейной корреляционной связи между признаками и отклоняется в пользу конкурирующей гипотезы при: 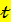набл 1,78

Если остатк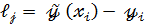и и 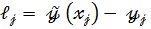не коррелированны между собой при 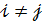, 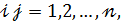то математическое ожидание величины 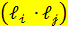равно нулю при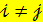

Если остатки 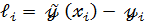и расчетные значения зависимой переменной 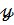не коррелированны, то:

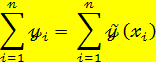
Если связь между факторами близка к функциональной, то определитель матрицы парных межфакторных коэффициентов корреляции близок к числу 0.

Если 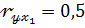; ; 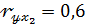s w:val="28"/></w:rPr><m:t>ОІ</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math" w:cs="Calibri"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>1</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 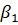=0,1; 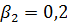; ( 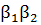- значения стандартизованных коэффициентов множественной линейной регрессии), то степень тесноты линейной связи признака – результата 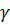с набором признаков – факторов 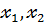учтенных в модели регрессии, можно оценить (с точностью 0,01) числом 0,41.

Если 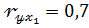; ; 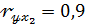; ; 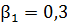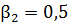( 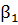, 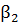- значения стандартизованных коэффициентов множественной линейной регрессии), то степень тесноты линейной связи признака – результата 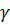с набором признаков – факторов 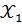, 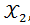учтенных в модели регрессии, можно оценить (с точностью 0,01) числом 0,81.

Если: объем выборки равен 10, 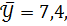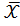= 6,9, 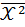= 59,9, 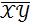= 41,1, то параметры 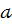, 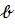уравнения парной линейной регрессии 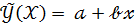являются решением системы уравнений:

Если коэффициент парной линейной корреляции 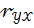равен 0,7 то доля вариации зависимого признака 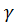, объясняемой изменением факторного признака 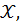составляет: 49%.

Если коэффициент парной линейной корреляции равен 0,6, то коэффициент парной линейной детерминации для тех же данных равен 0,36.

Если критическое (табличное) значение 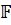- критерия (критерия Фишера) равно числу 6, 12, то нулевая гипотеза о статистической незначимости уравнения регрессии отклоняется в пользу конкурирующей гипотезы при условии .

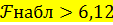Если сумма квадратов отклонений значений признака – результата 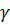от его среднего уровня равна 13,7 а остаточная сумма квадратов отклонений для уравнения множественной регрессии равна 1,3 то степень тесноты связи , признака 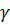с набором признаков – факторов включенных в модель регрессии, можно оценить (с точностью 0,01) числом 0,95.

Если сумма квадратов отклонений значений признака – результата 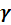от его среднего уровня равна 9,7 а сумма квадратов отклонений, объясненная вариацией признаков – факторов, учетных в модели регрессии, равна 7,3 то степень тесноты связи, признака 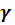с набором признаков – факторов можно оценить (с точностью 0,01) числом 0,87.

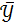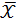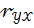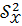
Если вычислены значения величин: , , , 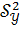по данным значениям признака – результата 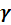и факторного признака 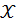, то уравнение парной линейной регрессии можно составить по правилу, выраженному равенством:

.

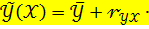
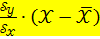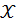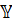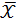Если средние квадратические отклонения наблюдаемых значений факторного признака и результирующего признака от и 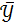равны 1,2 и 3,6 соответственно, а коэффициент линейной корреляции равен 0,5 то параметр 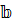в уравнении парной линейной регрессии 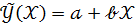равен 1,5.

Если: 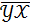=41,1 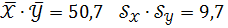то значение выборочного коэффициента парной линейной корреляции (с точностью 0,01) равно - 0,99.

Если 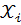, 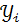- наблюдаемые значения признаков 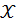и 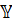соответственно,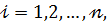 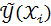- вычисление по уравнению регрессии значения признака 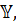то под остатками в регрессионном анализе понимают значения величин: =

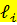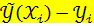
Если рассчитанные значения компонент временного ряда позволяют представить уровни ряда в виде суммы тенденции ряда, периодических колебаний и случайных колебаний, то построенная модель ряда называется аддитивной.

За последовательные 4 года по каждому кварталу вычислены суммы значений оценки сезонной компоненты:

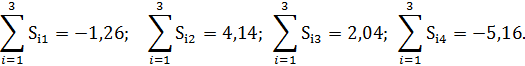
Скорректированные значения сезонной компоненты равны соответственно:

За последовательные 4 года по каждому кварталу вычислены суммы значений оценки сезонной компоненты:

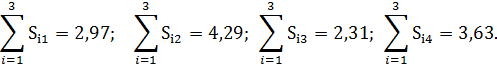
Скорректированные значения сезонной компоненты равны соответственно:

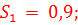
За последовательные 4 года по каждому кварталу вычислены суммы значений оценки сезонной компоненты:

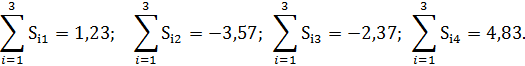
Скорректированные значения сезонной компоненты равны соответственно:

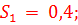
За последовательные 4 года по каждому кварталу вычислены суммы значений оценки сезонной компоненты:

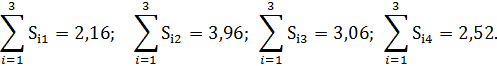
Корректирующий показатель для определения значений сезонной компоненты равен 0,975.

Задача дисперсионного анализа состоит в анализе (разложении) дисперсии значений зависимой переменной (признака - результата).

Зависимые переменные в системе одновременных эконометрических уравнений – это переменные эндогенные.

Значимость дополнительных факторов, включаемых в эконометрическую модель с целью улучшения модели, можно оценить с помощью частного F – критерия (критерия Фишера).

Значения выборочного коэффициента парной линейной корреляции обладают свойством

.

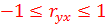Исследование стабильности (постоянства) дисперсии случайных отклонений в моделях регрессии сводится к проверке статистической гипотезы о равенстве:

1? Нулю дисперсии случайных отклонений в модели регрессии;

2? Нулю математического ожидания случайных отклонений в модели регрессии.

Исследование нелинейных модели регрессии на несмещённость случайных отклонений сводится к проверки статистической гипотезы:

1? 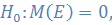M – математическое ожидание, Е – случайное отклонение;

2? 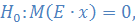M – математическое ожидание, Е – случайное отклонение.

Индекс детерминации характеризует долю дисперсии, объясняемую регрессией, в общей дисперсии признака – результата.

Измерителями степени тесноты корреляционной связи между признаком – результатом Y и признаками – факторами 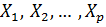являются показатели, вычисленные по n наблюдениям и в основе которых лежит значение величины:

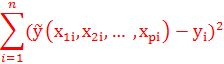
Исследование стабильности дисперсии случайного члена в регрессионной модели сводится к проверке статистической гипотезы о равенстве двух дисперсий (вычисленных по группе первых наблюдений и по группе последних наблюдений) с использованием статистики:

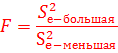
Где – Остаточные дисперсии.

Косвенный метод наименьших квадратов применим к вычислению структурных коэффициентов систем одновременных уравнений, выражающих только сверх идентифицирующие эконометрические модели.

Критерий Дарбина – Уотсона (DW) и коэффициент автокорреляции остатков ( 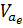) связаны равенством:

1? DW = 2(1- )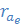

2? DW = 2(1- )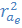

3? DW = 4(1- )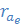

Косвенный метод наименьших квадратов применим к вычислению структурных коэффициентов систем одновременных уравнений, выражающих точно идентифицируемые эконометрические модели.

Критерием отбора наилучшей формы тренда временного ряда являются значения скорректированного коэффициента детерминации и коэффициента автокорреляции в остатках.

Матрица коэффициентов при эНдогенных переменных приведённой формы эконометрической модели может иметь вид:

Матрица коэффициентов при эКзогенных переменных приведённой формы эконометрической модели может иметь вид:

Матрица коэффициентов при эндогенных переменных в системе рекурсивных уравнений может иметь вид:

? ?

Модель изолированного временного ряда строится в том случаи, если даны несколько временных рядов и рассматривается

1? Один из них независимо от остальных;

2? Один из них как моделируемый объект, а остальные как его факторы.

Матрица парных коэффициентов корреляции – симметрична относительно главной диагонали.

Наиболее вероятно, что временной ряд характеризуется наличием периодических колебаний в динамике изучаемого показателя при следующих значениях коэффициентов автокорреляции:

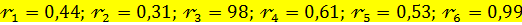
Недостающим элементом в формуле коэффициента парной линейной корреляции

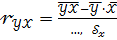является .

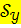Основой проверки значимости построенной регрессии и её параметров по общему F – критерию является анализ соотношения дисперсии.

Общая вариация зависимости переменной связана с факторной (объяснённой) суммой квадратов отклонений для регрессии и с остаточной суммой квадратов отклонений для регрессии равенством = +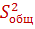

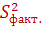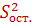
Остаточная сумма квадратов отклонений для регрессии вычисляется по формуле

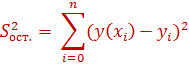
Общая сумма квадратов отклонений для регрессии вычисляется по формуле

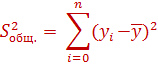
Оценивание качества уравнения регрессии состоит в проверке нулевой гипотезы о статистической не значимости индекса детерминации.

Параметр bj множественной линейной регрессии, значим, если доверительный интервал, покрывающий не включает число 0.

Параметры системы независимых эконометрических уравнений можно определить обычным (традиционным) методом наименьших квадратов

Приведенная форма некоторой структурной модели может быть выражена системой уравнений ,,,у-1.=2,𝑥-1.+,𝑥-2.+,𝑆-1.-,у-2.=,х-1.+1,5,𝑥-2.+,𝑆-2...

По двадцати семи наблюдениям за изменениями значений признаков 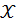и 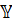значение парного коэффициента линейной корреляции составило 0,6. При проверке значимости степени тесноты линейной связи между признаками фактическое значение приемлемого статистического критерия составило 3,75.

По четырнадцати наблюдениям построено уравнение регрессии

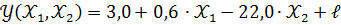и вычислены значения сумм квадратов отклонений: 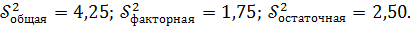На уровне значимости 0,05 табличное значение 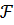- критерия равно 3,98. Построенная регрессионная модель незначима, т.к. фактическое значение 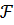- критерия равно 3,85.

Пусть: 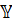- признак – результат; 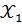; 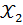– признаки – факторы. По исходным данным вычислены средние уровни признаков, средние квадратические отклонения значений признаков от средних уровней признаков 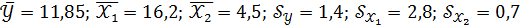и построено уравнение регрессии в стандартизованном масштабе 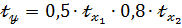+ и тогда теоретические (расчетные) значения признака – результата вычисляют по формуле:

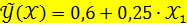+1,6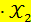

По двадцати пяти наблюдениям построено уравнение регрессии

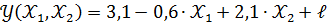Индекс множественной корреляции составил 0,7. На уровне значимости 0,05 табличное значение 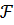- критерия равно 3,35. Построенная регрессионная модель значима, так как фактическое значение 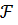- критерия равно 10,57.

Предопределенные переменные, влияющие на другие переменные, но не зависящие от них, это переменные: экзогенные.

Проверка статистической гипотезы об отсутствии гетероскедостичности случайного члена в регрессионной модели по выборкам большого объема требует вычисления статистики по формуле:

,𝒕-набл..=,𝒓-,𝒙-𝟏.𝒆.∗,-𝒏−𝟏 , .,𝒓-,𝒙-𝟏.𝒆.− коэффициент ранговой корреляции Спирмена

Показатель тесноты корреляционной связи данного фактора и признака – результата зависящий от других факторов, включенных в модель множественной линейной регрессии и от степени тесноты их связи с данным фактором – это коэффициент частной детерминации

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.