Занятие №80

Стр 1 из 2Следующая ⇒

Занятие №80

Тема:Формулы площади поверхностей.

План:

1.Площадь поверхности.

2. Площадь поверхности куба.

3. Площадь поверхности призмы.

4. Площадь прямоугольного параллелепипеда.

5. Площадь пирамиды.

6. Площадь боковой поверхности правильной усеченной пирамиды.

7. Площадь цилиндра.

8.Площадь конуса.

9.Площадь усеченного конуса.

1.Площадь поверхности – это сумма всех площадей поверхностей, которые составляют геометрическое тело. Площадь поверхности является числовой характеристикой поверхности и измеряется в квадратных единицах, например, в мм², см², м² и т.д.

Чтобы вычислить площадь поверхности геометрического тела, необходимо знать соответствующую формулу.

2. Площадь поверхности куба.

У куба шесть равных квадратных граней. Так как стороны квадрата равны, площадь квадрата равна a², где а – сторона. Так как у куба шесть равных квадратных граней, чтобы найти площадь поверхности, умножьте площадь одной грани (квадрата) на 6. Формула для вычисления площади поверхности куба:

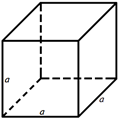S = 6а², где а – ребро куба (сторона квадрата).

3. Площадь поверхности призмы.

Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой поверхности призмы - сумма площадей ее боковых граней.

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы:

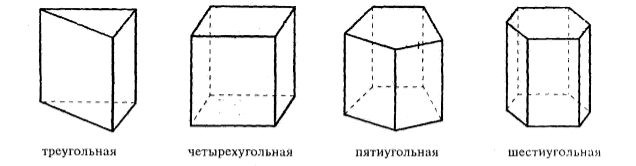S_бок=Ph, где P- периметр основания, h- высота призмы; основанием может быть любой многоугольник.

4. Площадь прямоугольного параллелепипеда.

У прямоугольного параллелепипеда шесть граней, противоположные грани являются равными. Поэтому формула для вычисления площади поверхности прямоугольного параллелепипеда включает значения трех разных ребер:

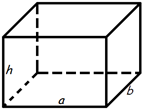S = 2ab + 2bh + 2ah или S = 2(ab + ah + bh),

где S - площадь прямоугольного параллелепипеда а – ширина, b – длина, h – высота. Данная формула суммирует площади всех граней.

5. Площадь пирамиды.

Площадью полной поверхности пирамиды называется сумма площадей всех ее граней (т.е. основания и боковых граней), а площадью боковой поверхности пирамиды - сумма площадей ее боковых граней.

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему:

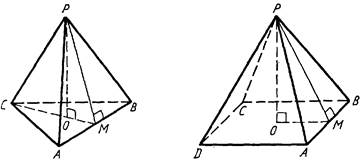S_бок= 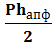_,где P- периметр основания, h_апф- высота боковой грани пирамиды (апофема).

6. Площадь боковой поверхности правильной усеченной пирамиды.

Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметра оснований на апофему:

S_бок= 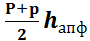_,где P,p - периметры оснований, h_апф- высота боковой грани усеченной пирамиды (апофема).

Самостоятельно решить задачу по чертежу.

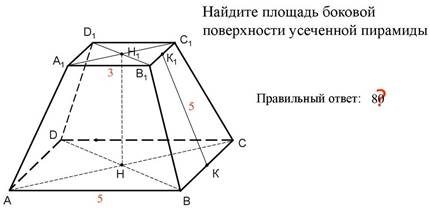
7. Площадь цилиндра.

Площадь боковой поверхности цилиндра равна произведению периметра его основания на высоту:S_бок=Ph, где P- периметр основания, h- высота цилиндра. 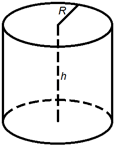В основании цилиндра лежит круг, значит, периметром основания является длина окружности, которая находится по формуле: C=2πR. Следовательно, формула площади боковой поверхности цилиндра имеет вид: S_бок=2πRh.

Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.

12 Следующая ⇒