Декартова прямоугольная система координат в пространстве.

2. Декартова прямоугольная система координат в пространстве.

Совокупность прямоугольного базиса и начала координат называют прямоугольной системой координат в пространстве.

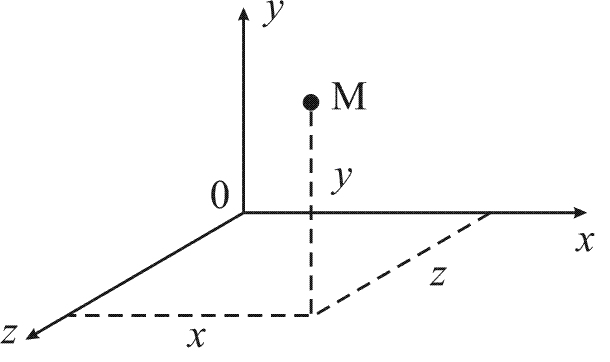3. Координаты точки и вектора в пространстве.

Любая точка М(x; y; z) в пространстве имеет 3 координаты: х-абсцисса, у-ордината, z-аппликата.

Любой вектор ={х; у; z} или { х₂ – х₁, у₂ – у₁, z₂ – z₁} в пространстве также имеет 3 координаты:

х- абсцисса, у- ордината, z- аппликата.

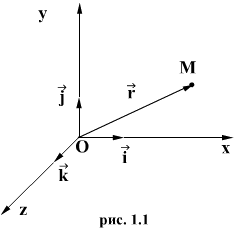Радиус-вектором называют вектор, проведённый из начала координат в произвольную точку пространства.Радиус-вектор имеет координаты точки, в которую он проведён.

= ={х; у; z}

Координаты вектора выражаются через координаты его начала А(х₁; у₁; z₁) и конца В(х₂; у₂; z₂):

{ х2 – х1, у2 – у1, z2 – z1}.

Правило 1. Для определения координат вектора АВ нужно от координат конца вектора вычесть координаты начала.

Координаты равных векторов равны.

4.Разложение вектора по трём некомпланарным направлениям:

а) разложение радиус-вектора по базису

Пусть – единичный вектор оси абсцисс, - единичный вектор оси ординат, - единичный вектор оси аппликат. Радиус-вектор = можно разложить по единичным векторам:

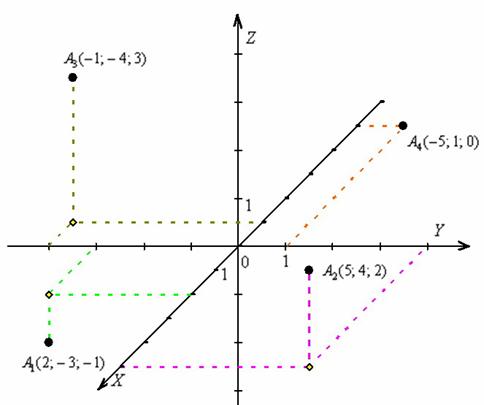
Построение точки в пространстве

Для построения точки в пространстве необходимо:

1) Построить прямоугольную систему координат в пространстве Охуz.

2) Отложить первые две координаты на соответствующих осях и провести их проекции;

3) Выполнить параллельный перенос третьей координаты в точку пересечения проекций;

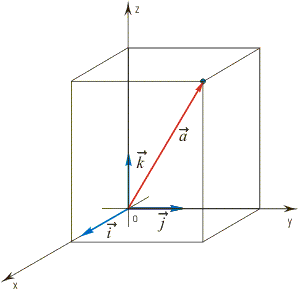
Построение радиус-вектора в пространстве

Для построения радиус-вектора в пространстве необходимо:

1) Построить прямоугольную систему координат в пространстве Охуz.

2) Отложить первые две координаты конца вектора на соответствующих осях и провести их проекции;

3) Выполнить параллельный перенос третьей координаты в точку пересечения проекций;

4) Соединить полученную точку с началом координат и обозначить искомый вектор.

Ссылка на сообщество МАТЕМАТИКА в контакте https://vk.com/club194177059

⇐ Предыдущая 12