
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Выражение координат середины отрезка через координаты его концов
Выражение координат середины отрезка через координаты его концов

Ромб. Свойства и признаки ромба
Ромб – это параллелограмм, у которого все стороны равны.
Свойства:
1) Все высоты равны между собой
2) Диагонали перпендикулярны
3) Диагонали являются биссектрисами
Доказательство слишком уж простое
4) Диагонали делят ромб на 4 равных прямоугольника
Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника.

Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции.

Параллелограмм – это четырехугольник, у которого противолежащие стороны параллельны.
Свойства:
1) Диагональ делит пар-м на 2 равных треугольника.
2) Сумма соседних углов пар-ма равна 180◦.
3) Противолежащие углы равны; противолежащие стороны равны.
4) Биссектриса угла пар-ма отсекает от него равнобедренный треугольник.
5) Биссектрисы, проведенные из противоположных углов пар-ма, параллельны или совпадают.
6) Биссектрисы, проведенные из соседних углов пар-ма, перпендикулярны.
7) Диагонали пар-ма пересекаются и точкой пересечения делятся пополам.
Радиус описанной окружности правильного многоугольника: 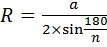
Радиус вписанной окружности правильного многоугольника: 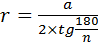
Sпар-ма=a*ha
Sтр=a*b*sin α
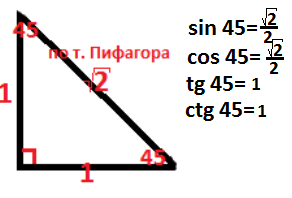
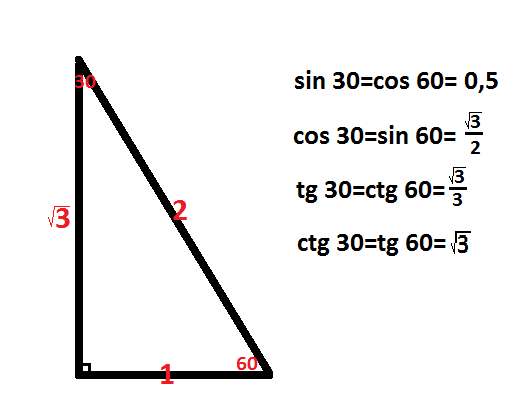
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|