Таблица 1

Таблица 1

					…
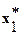
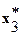
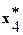
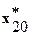
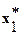
		0.98286	4.4857	0.6369	…	1.8222
	0.6611		2.6279	0.8887	…	2.9414
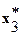
	10.221	7.369		10.845	…	2.8603
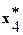
	0.4823	0.60722	4.9626		…	1.4164
…	…	…	…	…	…	…
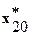
	0.8513	0.96772	3.2227	0.93173	…

При этом применялись специальные программные и аппаратные средства: динамический микрофон AKG D77 S и ламповый микрофонный предусилитель ART TUBE MP Project Series USB. Частота дискретизации встроенного АЦП была установлена равной 8 кГц – общепринятое значение при обработке устной речи. Продолжительность записи составила около полутора минут.Это был художественный текст, взятый из первой главы романа А.С. Пушкина "Капитанская дочка". Длина одного сегмента данных составляла n = 80 отсчетов, или 10 мс по времени.А для расчета коэффициентов авторегрессии 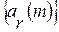в (4) использовалась рекуррентная процедура Берга-Левинсона [7] с высокой скорость сходимости. Полученное множество 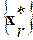совместно с выражениями (3), (4) и определяло в конечном итоге принятое по критерию МИР (2) решение в пользу одной из фонем 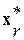по каждой очередной ЭРЕ 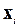в составе анализируемого речевого сигнала .

Распознавание изолированных слов. Мысленно разобьем анализируемый составной сигнал , теперь длиной в одно слово, на некоторую последовательность фонем 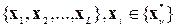длиной в одну ЭРЕ каждая. Здесь L – длина изолированного слова, выраженная в числе входящих в него фонем. При этом некоторые фонемы в нем могут повторяться. В качестве иллюстрации на рис.1 показаны временные диаграммы двух слов разной длины.

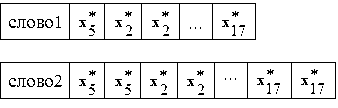
Рис. 1. Временные диаграммы слов

В задаче АРР общего вида (2) сигналу с входа 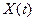противопоставляется R альтернатив из множества эталонных слов 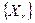. Каждое из таких слов-эталонов предварительно разбивается на соответствующую последовательность фонем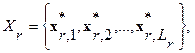 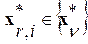. Предположим сначала, что все они согласованы по своей длине с длиной L анализируемого слова. При учете статистической независимости выделенных фонем в слове его АКМ размера 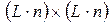имеет блочно-диагональную структуру и состоит из L квадратных 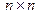АКМ составляющих слова фонем: 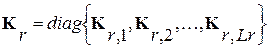. В таком случае, как это следует из (1), рассогласование Кульбака-Лейблера между двумя рассматриваемыми словами

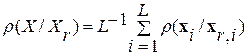(7)

определяется суммой ИР 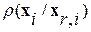между парами их фонем на одноименных позициях в слове.

Все выше сказанное сохраняет свою справедливость и в общем случае разной длины 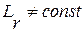каждого отдельного слова, например, из-за разного темпа речи одного или разных дикторов. На нашем рис. 1 отображена именно эта ситуация. Во всех таких случаях перед применением выражения (7) входной сигнал X и каждый сигнал-эталон 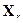должны быть предварительно выровнены по темпу речи. Для этого на практике применяются специальные алгоритмы, основанные, как правило, на методе динамического программирования [9].

Таким образом, распознавание слов по МОФ в общем случае реализуется на основе многоканальной обработки, в которой число каналов R определяется количеством слов-эталонов. При этом в каждом r-м канале используется набор из 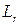обеляющих фильтров, настроенных на последовательные стационарные участки (фонемы) соответствующего эталонного слова. Решение (2) принимается по критерию минимума суммы решающих статистик (7) по всем L сегментам анализируемого слова.

Метрические свойства решающей статистики МИР. Рассмотрим случай R>>1, когда решается задача АРР с объемом эталонного словаря (ЭС) в сотни и даже тысячи слов. В указанных условиях практическая реализация МОФ по схеме R-канальной обработки (3)…(7) наталкивается на очевидную проблему вычислительной сложности. Выполнение проверки гипотез по схеме (7), включающей в себя предварительное выравнивание анализируемых слов по длительности или темпу речи, становится в данном случае непреодолимым препятствием для работы системы АРР в режиме реального времени. В поиске путей решения указанной проблемы за счет отказа от сплошного перебора ЭС и состоит центральная задача настоящей работы.

Прежде всего, отметим метрические свойства решающей статистики МИР 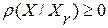с равенством ее нулю лишь в идеальном случае совпадения входного и эталонного сигналов. Поэтому вначале преобразуем критерий МИР (2) к упрощенному (в его практической реализации) виду

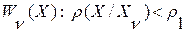. (8)

Здесь 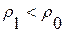- это порог для допустимой величины ИР по Кульбаку-Лейблеру на множестве одноименных слов за счет известной вариативности устной речи. Значение такого порога нетрудно установить опытным путем [9]. Например, в условиях предыдущего эксперимента (табл. 1) на уровне значимости критерия (8) 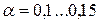было получено приближенное равенство 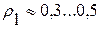. Это примерно в два раза меньше значения «информационного радиуса» 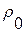в (5) при определении множества реализаций каждой отдельной фонемы. По своей сути выражение (8) определяет условие «останова» при переборе альтернатив в рамках проверочной процедуры по МОФ (3)…(7).

Таким образом, при принятии решения на основе принципа МИР (2) требуется просматривать не весь словарь целиком, а вычислять величину ИР лишь до тех пор, пока оно не будет меньше некоторого порогового уровня. Нетрудно понять, что само по себе указанное обстоятельство позволит сократить объем перебора в среднем на 50%. Иными словами, благодаря использованию правила останова (8) удается в два раза сократить объем выполняемых вычислений и этим существенно ослабить проблему практической реализуемости АРР в режиме реального времени. В этом состоит принципиальное преимущество МОФ по сравнению со всеми его наиболее известными аналогами, такими как группа методов на основе скрытых марковских моделей (СММ-методы) и другие, в которых применяются классические (байесовские) критерии: минимума среднего риска, максимума апостериорной вероятности и др. Между тем, как это выясняется ниже, рассмотренный выигрыш в производительности далеко не исчерпывает всех преимуществ МОФ и принципа МИР в задаче распознавания образов.

Действительно, общая формулировка задачи (2) позволяет рассматривать ее как задачу оптимизации и применять алгоритмы поиска оптимального решения с заданным условием останова (8). В такой задаче на множестве эталонных слов 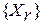требуется найти такое слово 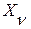, которое будет минимизировать статистику МИР. В таком случае метод, сводящийся к полному перебору ЭС, является одним из множества известных методов оптимизации систем. Главным препятствием для применения в нашей задаче более эффективного оптимизационного метода является то, что, во-первых, задача относится к области дискретной математики и, во-вторых, в ней требуется найти глобальный минимум решающей статистики (2). По-видимому, наиболее обоснованным способом поиска глобального экстремума в указанных условиях можно считать метод случайного поиска и, в частности, его наиболее распространенную разновидность – генетический алгоритм (ГА) [10]. В нашем случае генотипом для ГА будет номер r слова из ЭС, а фенотипом – выражение (2). Возможности применения ГА будут подробно описаны ниже в результатах экспериментальных исследований.

Предварительно же можно отметить следующий главный недостаток ГА в рамках решения поставленной задачи. Перебор организуется только по номеру эталонного слова в ЭС. То есть информация о самих словах, рассогласованиях между ними, в стандартном ГА никак не учитывается. На помощь снова приходит принцип МИР. Действительно, на основе того же выражения (8) мы можем сформулировать критерий останова работы ГА. В этом случае появляется гарантия того, что решение задачи, если оно существует (то есть если эталон входного слова присутствует в словаре), с помощью ГА будет найдено. Естественным развитием этой идеи может служить предложенный ниже метод направленного перебора (МНП) словаря, в котором метрические свойства решающей статистики МИР (8) используются в наиболее полной степени.

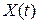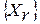Идея МНП. Следуя общей схеме вычислений по МОФ (3)…(7), сведем задачу автоматического распознавания слова к проверке N первых вариантов из R альтернатив при условии N<<R. Если, по крайней мере, одна из них 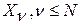, отвечает требованию останова (8), процесс поиска оптимального решения по критерию МИР (2) на ней и завершается. Однако в общем случае можно предположить, что ни одна из первых N альтернатив проверку (8) не проходит. В таком случае можно проверить вторые N эталонных слов из множества 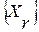, потом третьи и т.д. – до момента выполнения условия (8). Но есть и иной, предпочтительный, вариант поведения.

Расставим слова из нашей контрольной выборки 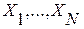в порядке убывания их ИР 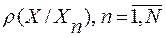. В результате будем иметь упорядоченную (ранжированную) последовательность эталонных слов вида 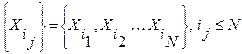. Соответствующая последовательность 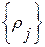их ИР 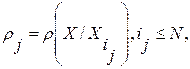будет иметь характер монотонно убывающей зависимости. Ее вид, в частности, скорость убывания, будет зависеть как от состава контрольной выборки эталонов 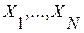, так и ее теоретико-информационных характеристик, в частности, от величины взаимных информационных рассогласований (ВИР) 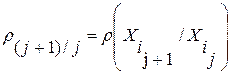между парами соседних элементов в упорядоченной контрольной выборке 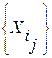. Проиллюстрируем указанную зависимость с помощью специально для этого нами созданного экспериментального ЭС.

При его формировании в качестве базы эталонных данных использовался тот же набор из 20 фонем , который был положен в основу построения табл.1. На его основе путем простого перебора разных сочетаний фонем было сформировано множество эталонных слов 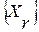большого объема R=10000. В нем каждое слово отображалось определенной последовательностью фонем длиной в одну ЭРЕ, как это было показано на рис.1. Их сочетания в экспериментальном варианте словаря устанавливались случайным образом. Тем самым достигались наиболее жесткие условия для последующего автоматического распознавания слов X(t). При этом длина каждого слова варьировалась также случайным образом в рабочем интервале ее значений: от 10 до 20 ЭРЕ. А для их выравнивания по динамике применялась стандартная процедура [9].

При этом на первом этапе вычислений состав контрольной выборки 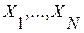был выбран нами наугад, ее объем был установлен равным N=100. Для вычисления ИР (7) использовались данные предварительного фонетического анализа из табл.1. По результатам вычислений была получена упорядоченная контрольная выборка 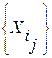. Ее фрагмент из 30 последних элементов 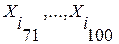отображен на рис. 2,а в виде графика зависимости их ИР 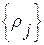относительно определенного слова на входе 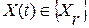. Здесь же для сравнения на рис.2,б (сплошная линия) представлен график соответствующей зависимости величины ВИР 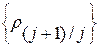. Хорошо, в частности, видно, что данная последовательность вслед за последовательностью ИР 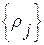для элементов упорядоченной контрольной выборки 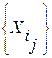имеет характер затухающих колебаний.

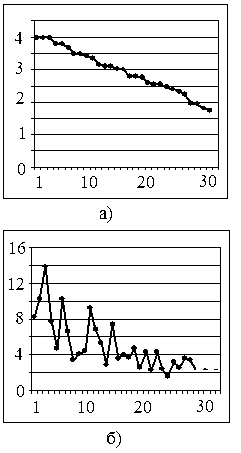
Рис.2. Последовательность ИР

Указанное наблюдение усиливается результатами экстраполяции последовательности значений ВИР на рис.2б (штриховая линия) за границы контрольной выборки по формуле оценки линейного прогнозирования P-го порядка:

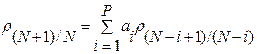(9)

Здесь 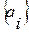– вектор АР-коэффициентов. При этом, как и ранее, для АР-анализа использовалась рекурсивная вычислительная процедура Берга-Левинсона [7], а порядок авторегрессии был установлен равным P=5. Отсюда и вытекает главная идея МНП: использовать последний элемент из упорядоченной контрольной выборки 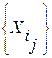как наилучшее приближение к искомому слову 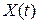в роли точки отсчета для поиска наиболее подходящих «кандидатов» в очередную контрольную выборку. При этом данные экстраполяции ВИР (9) могут служить ориентиром для определения максимально допустимой различий слов-эталонов из новой контрольной выборки по отношению к «точке отсчета» в теоретико-информационном смысле. Проиллюстрируем сказанное с помощью диаграммы поисковой процедуры МНП на рис.3.

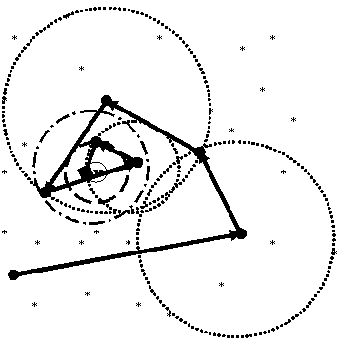
Рис. 3. Поисковая процедура МНП

Здесь звездочками обозначены все имеющиеся слова-эталоны, буквой X – входное слово, а ромбиком – наиболее близкий к 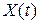эталон. Он и определяет искомое оптимальное решение задачи. Траектория поиска отображается на рисунке ломаной направленной линией. Жирными точками на ней обозначена последовательность наиболее близких к оптимуму слов после нескольких подряд этапов вычислений. Окружностями здесь отмечены границы соответствующих контрольных точек-выборок 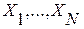. Их радиусы определяются согласно выражению (9). Хорошо видно, что траектория поиска имеет вид скручивающейся спирали.

Синтез алгоритма. Следуя определению ИР (7), (3), (4) и используя процедуру динамического выравнивания слов-эталонов разной длины, составим 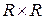-матрицу 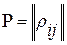значений ИР 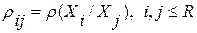. Эту весьма сложную в вычислительном отношении операцию требуется выполнить лишь раз: на предварительном этапе вычислений – для каждого конкретного ЭС.

Сначала, как это было описано выше, зададимся в пределах имеющегося 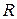-словаря произвольной первой контрольной выборкой 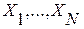некоторого фиксированного объема N, по ней получим ранжированный по критерию МИР (2) ряд данных 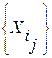и, наконец, находим из него первый локальный оптимум . На этом завершается первый этап вычислений. Переходя ко второму этапу, для выделенного слова-эталона по матрице 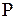найдем множество из M<R слов 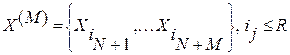, находящихся от слова на «расстоянии» (7), не превышающем порогового значения 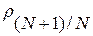, или

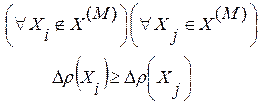(10)

Здесь 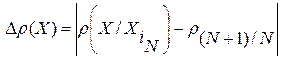- отклонение спрогнозированного рассогласования 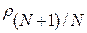от ИР между словом 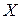и словом .

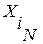На рис.3 каждое такое множество ограничивается соответствующей окружностью с центром в точке . Добавим к этому множеству еще один, (M+1)-й элемент 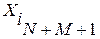из числа не попавших в состав контрольной выборки по результатам предыдущего этапа вычислений. Этим мы вносим в поисковую процедуру определенный элемент случайности как способ достижения глобального оптимума за конечное число шагов оптимизации (этапов вычислений).

В результате получаем вторую контрольную выборку слов-эталонов 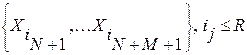, для анализа. Далее все вычисления первого этапа циклически повторяются. Повторяются до тех пор, пока на некотором K-м этапе не будет выполнено условие останова

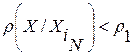. (11)

На рис.3 в такой момент входное слово оказывается в пределах границ множества контрольных точек последнего этапа вычислений. Решение здесь принимается в пользу наиболее близкого образа 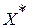. Или, в худшем случае, после перебора всех альтернатив из словаря 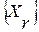в отсутствие решения (11) делается вывод о том, что прозвучавшее (входное) слово в данном ЭС отсутствует и необходимо задействовать режим переспроса. В общем же случае, суммарное число 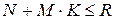выполняемых согласно (11) проверок может существенно выигрывать по сравнению с объемом используемого ЭС. В этом и состоит эффект направленного перебора.

Таким образом, система выражений (7)…(11) и определяет, в конечном итоге, предлагаемый метод в задаче АРР.

Результаты экспериментальных исследований.После составления описанного выше экспериментального ЭС достаточно большого объема R=10000 был поставлен и 100 раз выполнен следующий эксперимент. На основе некоторого (каждый раз разного) слова-эталона 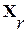путем дублирования или, напротив, удаления части его ЭРЕ каждый раз создавалось некоторое анализируемое слово 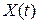. На нашем предыдущем рис.1 представлены типичные диаграммы именно такой пары слов 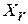и 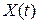. В каждом случае решалась задача автоматического распознавания слова 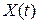из множества всех его допустимых альтернатив 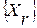. Сначала для этого применялся ГА. Его параметры были выбраны следующим образом: количество особей в начальной популяции N=128, количество потомков M=80. Порог 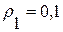для правила останова (8) был выбран, исходя рекомендаций работы [8]. В этом варианте ГА дал точное решение 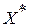в 98% случаев проверок гипотез. При этом на каждое такое решение в среднем потребовалось проверить (перебрать) 5700 слов, или 57% от объема всего ЭС. При учете вычислительной сложности обязательной в таких случаях процедуры выравнивания слов по динамике подобное ускорение обработки (почти в 2 раза) представляется, на первый взгляд, весьма существенным достижением. Однако данный вывод требует уточнения.

Для этого рассмотрим на рис.4 (график ГА) гистограмму количества осуществляемых в данном случае проверок слов (в процентах). Хорошо видно, что она имеет приблизительно прямоугольный вид во всей своей области определения от 0 до R. По сути это означает равновероятно случайный поиск. Примерно тот же результат мы будем иметь по результатам сплошного перебора ЭС с автоматическим остановом по правилу (8). Таким образом, применение ГА почти ничего не дает в решаемой задаче АРР. Совсем иное дело – МНП.

Его гистограмма при тех же значениях параметров N=128, M=80 и 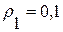алгоритма (7)…(11) показана на том же рис.4 (график МНП). Здесь среднее количество проверок составило примерно 26% от объема ЭС. С вероятностью 80% МНП это количество не превышает 5000 или 50% от общего числа слов-эталонов для проверки. При этом в 100% случаев было получено абсолютно точное решение .

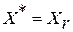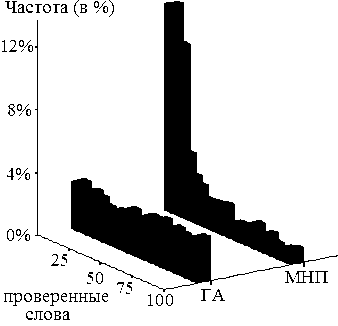
Рис. 4. Гистограммы количества проверок слов

Заключение. Вопрос о повышении скорости вычислений вызывает повышенный интерес среди специалистов как в области теории, так и практики АРР. Действительно, в тех случаях когда объем рабочего словаря начинает составляет сотни и тысячи единиц, большинство известных алгоритмов, работающих на основе сегментирования на отдельные фонемы и их последующего выравнивания по динамике [9], не могут быть реализованы в режиме реального времени. Поэтому решению проблемы вычислительной сложности для больших словарей в последние годы и уделяется повышенное внимание. В представленной работе для этого предложен новый метод: направленного перебора, основанный на теоретико-информационном подходе и отталкивающийся от метрических свойств решающей статистики МИР [1]. При этом принципиальное значение при переборе альтернатив имеет правила автоматического останова (7). В самом невыгодном варианте своего применения оно сокращает объем вычислений в среднем в 2 раза. А при использовании предложенного метода в формулировке (11) суммарный выигрыш в вычислительной сложности алгоритма возрастает почти до 4 раз. При этом не утрачивается (по сравнению со сплошным перебором ЭС) и качество достигаемого по МНП решения .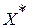

Таким образом, благодаря проведенному исследованию предложен новый метод АРР на основе принципа МИР, обладающий широкими функциональными возможностями и высокими эксплуатационными свойствами.

Библиографический список

1. Савченко В.В., Савченко А.В. Принцип минимального информационного рассогласования в задаче распознавания дискретных объектов // Известия вузов России. Радиоэлектроника. 2005. Вып.3. С.10-18.

2. Савченко В.В. Информационная теория восприятия речи. // Известия вузов России. Радиоэлектроника. 2007. Вып.6. С.3-9.

3. Савченко В.В., Акатьев Д.Ю. Теоретико-информационное обоснование метода обеляющего фильтра в задачах автоматического распознавания речи. // Системы управления и информационные технологии. 2008. №1 (31). С.21-30.

4. Савченко В. В., Акатьев Д. Ю., Карпов Н. В.Автоматическое распознавание элементарных речевых единиц методом обеляющего фильтра. // Известия вузов. Радиоэлектроника. 2007. Вып.4. С.11-19.

5. Кульбак С.Теория информации и статистика. М.: Наука, 1967, 408 с.

6. Савченко В.В. Различение случайных сигналов в частотной области // Радиотехника и электроника. 1997. Т.42, №4. С. 426–431.

7. Марпл С.Л.-мл. Цифровой спектральный анализ и его приложения. М.: Мир, 1990, 584 с.

8. В.В.Савченко, Карпов Н.В. Анализ фонетического состава речевого сигнала методом переопределенного дерева. // Системы управления и информационные технологии 2008. №2 (32), C. 297-303.

9. Д.Ю. Акатьев, И.В. Губочкин, В.В.Савченко. Автоматическое распознавание изолированных слов методом обеляющего фильтра с сегментированием и амплитудным ограничением сигналов переспросом // Изв. вузов России. Радиоэлектроника. 2007. Вып. 5. С. 11–18.

10. Goldberg, D.: Genetic Algorithms in search, optimization, and machine learning. Addison–Wesley, 1989.

⇐ Предыдущая 12