Ответ: След матрицы A равен 4. Операции с матрицами

Ответ: След матрицы A равен 4

Единичной называется такая квадратная матрица, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю:

(3) Е =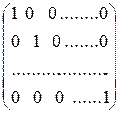

Различаются также матрицы, имеющие только одну строку или один столбец.

Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.

Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

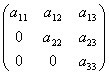Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, 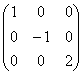или .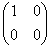

Операции с матрицами

1. Сумма матриц: А + В.

Складывать можно только матрицы одного размера. При сложении двух матриц одного размера получается матрица того же размера, элементы которой равны сумме элементов слагаемых матриц, стоящих на соответствующих местах.

Пример.

Пусть 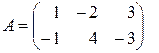, 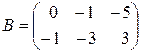. Тогда

А + В = + =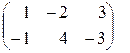

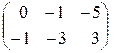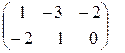
Аналогично определяется вычитание матриц:

А – В = – = .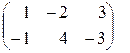

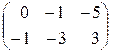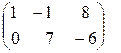2. Умножение числа на матрицу.

При умножении числа на матрицу каждый ее элемент умножается на это число.

Пример.

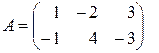, тогда .

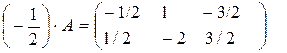Матричные уравнения

Это уравнения, в которых неизвестной является матрица.

Пример. Даны матрицы 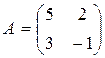и 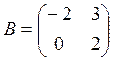. Найти матрицу 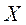, удовлетворяющую следующему матричному уравнению .

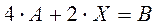Решение. Сначала рассматриваем это уравнение как обычное числовое и находим формулу для 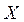. Затем действия, предписываемые этой формулой, выполняем по правилам действий с матрицами. Решая обычным способом уравнение 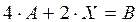, получаем 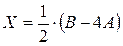. По правилу умножения числа на матрицу 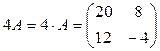, по правилу вычитания матриц 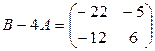. Наконец, по правилу умножения числа на матрицу неизвестная матрица .

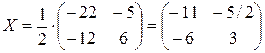3. Умножение матриц :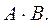

Далеко не все матрицы можно перемножать.

Матрицы A и B (порядок следования важен!) называются согласованными, если число столбцов матрицы A равно числу строк матрицы B.

Таким образом, если порядок матрицы A равен m × p , то порядок согласованной с ней матрицы B должен быть равен p × n. Перемножать можно только согласованные матрицы (отметим, что квадратные матрицы одного порядка всегда согласованы).

Произведением двух согласованных матриц A (размера m × p) и B (размера
p × n ) называется матрица C (размера m × n) , элементы которой вычисляются по правилу: элемент 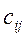матрицы С равен сумме попарных произведений элементов i-ой строки матрицы А и j-го столбца матрицы В:

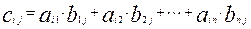
Например, если требуется получить элемент c₂₁, то нужно вторую строку матрицы A "умножить" на первый столбец матрицы B. Рассмотрим конкретные матрицы

, .

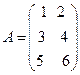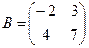Число столбцов матрицы A и число строк матрицы B равны 2, значит, A и B согласованы, причем матрица А∙В будет размера 3х2 . Тогда по определению произведение этих матриц А∙В вычисляется следующим образом:
.
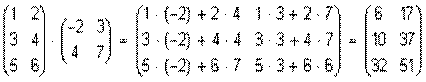Найти в этом случае произведение B∙A невозможно, т.к. матрицы B и A не согласованы. Отсюда следует, что если две матрицы можно перемножить в одном порядке, то это не означает, что их можно перемножать в другом порядке. Можно показать, что в общем случае, даже когда произведения AB и BA определены, они не всегда дают одну и ту же матрицу (даже размерности матриц АВ и ВА могут быть разными).

Свойства операции умножения матриц.

А(В+С)=АВ+АС;
(А+В)С=АС+ВС;
k(АВ)=(kА)В = А(kВ), k - некоторое число;
А(ВС)=(АВ)С;
А · Е =Е·А =А, где Е – единичная матрица.

n×n n×n n×n

Пример. Пусть 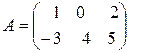, 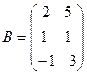. Тогд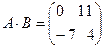а , а

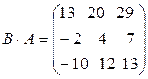(проверьте!). Таким образом .

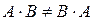Это не значит, что вообще не существует двух таких матриц А и В, для которых АВ=ВА.

Если для пары матриц А и В это свойство все же выполняется, то такие матрицы называются перестановочными (или коммутативными). Например, коммутативными будут матрицы А = 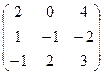и В = .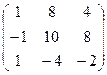

Легко перемножением в том и обратном порядке убедиться, что АВ = ВА = 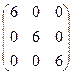. Отметим, что квадратные матрицы можно перемножать только если они одного порядка.

Можно указать одну особенную матрицу, которая перестановочна с любой квадратной матрицей. Это введенная выше единичная матрица. Легко в общем виде показать, что для любой квадратной матрицы А имеет место:

А·Е = Е·А = А .

⇐ Предыдущая 12