
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лекция 1. Матрицы, определители. Элементарные преобразования матрицы.
Лекция 1. Матрицы, определители. Элементарные преобразования матрицы.
 Матрицей называется прямоугольная таблица чисел . Обозначаются прописными буквами А, В, С, …..
Матрицей называется прямоугольная таблица чисел . Обозначаются прописными буквами А, В, С, …..
Общий вид матрицы, содержащей m строк и n столбцов:
(1) А = 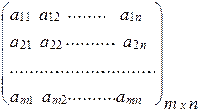
Внизу справа при необходимости подписываются размеры матрицы: m – количество строк, n – столбцов.
 Числа
Числа 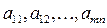 , составляющие матрицу, называются элементами матрицы.
, составляющие матрицу, называются элементами матрицы.
Матричные элементы обычно обозначаются той же буквой (только строчной), что и сама матрица, а индексы показывают место элемента матрицы в матрице: первый индекс указывает номер строки, а второй – номер столбца, на пересечении которых находится данный матричный элемент. Например, для матрицы
А = 
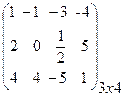 элементы
элементы 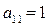 ,
, 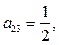 ….
….
Матрицы (так же как и числа) можно вычитать, складывать, перемножать. Поэтому среди матриц есть аналоги нуля и единицы. Нулевой матрицей называется матрица, все элементы которой равны нулю. Она имеет следующий вид и обозначение:
О = 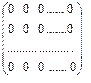
Если в матрице (1) поменять местами строчки и столбцы (т.е. первую строчку сделать первым столбцом, вторую строку – вторым столбцом и т.д.), то полученная матрица носит название транспонированной по отношению к исходной матрице и обозначается 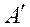 или
или 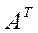 :
:
А’ = 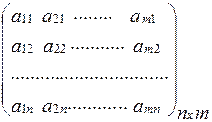
Квадратная матрица – матрица, число строк и столбцов у которой совпадают. Общий вид квадратной матрицы:
(2) А = 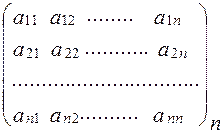
Числа 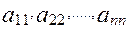
 называются главной диагональю квадратной матрицы.
называются главной диагональю квадратной матрицы.
След матрицы - это сумма элементов главной диагонали квадратной матрицы: Sp( A ) = a11 + a22 + ... + aii + ... + ann
Дана квадратная матрица A размерностью 3
А = 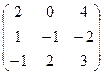
Решение:
Чтобы вычислить след исходной матрицы, нужно сложить элементы на главной диагонали:
Sp( A ) = 2 - 1 + 3 = 4
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|