АНО ВО МОСКОВСКИЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ

Стр 1 из 2Следующая ⇒

АНО ВО МОСКОВСКИЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ

Факультет: Экономики и управления

Кафедра: Прикладная информатика

Контрольная работа

По дисциплине

‹‹Изучение прогнозирование спроса››

Выполнил студент заочного отделения

гр.Тд401_311

Акрамов Зохир Муртазоевич

Проверяла

Мамаева Наталья Владимировна

Москва 2019 г

Вариант 1.

Задача 1.

По данным варианта (из файла «Тренд сезонные модели (данные для первой задачи.xls)») необходимо построить тренд-сезонную модель:

1. построить график и определить вид модели;

2. провести сглаживание ряда методом скользящей средней (выбор интервала сглаживания обосновать);

3. рассчитать средние индексы сезонности, при необходимости осуществить корректировку;

4. построить график сезонной волны;

5. найти сезонную компоненту временного ряда;

6. провести десезонализацию данных;

7. определить методом аналитического выравнивания тенденцию полученного ряда (выбор наилучшей модели тренда осуществить на основе расчета значений известных критериев адекватности);

8. определить расчетные значения по уравнению тренда;

9. определить значения случайной компоненты;

10. по построенной модели рассчитать прогнозные значения на 1 год вперед.

11. на одной диаграмме построить график исходных значений и прогнозных

Построим график данного временного ряда. Анализ графика позволяет сделать вывод о наличии в изучаемом временном ряде, во-первых, линейной тенденции, во-вторых, сезонных колебаний периодичностью в двенадцать месяцев (m=12).

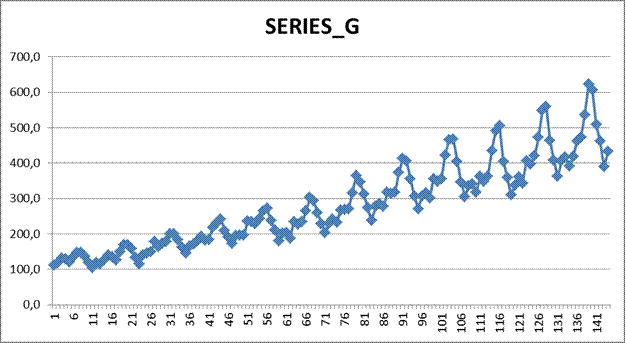
Сезонная колебаемость в рядах динамики может иметь аддитивный и мультипликативный характер.

Т.к. сезонная вариация не является константой, увеличивается с возрастанием значений тренда, то для анализа лучше подходит модель с мультипликативной компонентой, в которой значения сезонной компоненты представляют собой определенную долю трендового значения.

Общий вид мультипликативной модели выглядит так:

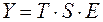Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой ( 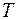), сезонной ( 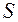) и случайной ( 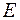) компонент.

Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:

1. Просуммируем уровни ряда последовательно за каждые двенадцать месяцев со сдвигом на один момент времени

2. Разделив полученные суммы на 12, найдем скользящие средние. Полученные таким образом выровненные значения уже не содержат сезонной компоненты.

3. Приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние.

Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние.

месяц, t

12 Следующая ⇒