Хелпикс

Главная

Контакты

Случайная статья



Это же задание выполнить с помощью ИС Eureka и Scilab.

⇐ ПредыдущаяСтр 2 из 2


ЗАДАНИЕ 3

Методом средних точек определить вид зависимости и найти коэффициенты выбранной зависимости методом наименьших квадратов по таблице из задания 2

 

ЗАДАНИЕ 4

 

По таблице из задания 2 вычислить значение функции в точке x* = m+n+ Nст/30

а) с помощью интерполяционного полинома Лагранжа, используя первые три точки таблицы;

б) с помощью интерполяционного полинома Ньютона, используя все точки таблицы.

Это же задание выполнить с использованием ИС Eureka и Scilab.

ЗАДАНИЕ 5

С помощью ИС Eureka и Scilab вычислить определенный интеграл

 a)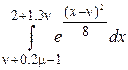    

b)

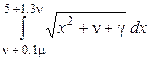
 Тот же интеграл вычислить по обобщенным формулам левых прямоугольников, правых прямоугольников, трапеций и Симпсона, взяв шаг интегрирования равным одной десятой длины интервала интегрирования.

ЗАДАНИЕ 6

 

Методом Эйлера решить задачу Коши для обыкновенного дифференциального уравнения первого порядка

a) 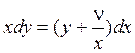         b)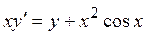

                 

                    

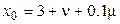
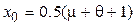
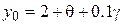
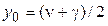
Взять шаг h = 0.2. Сделать три итерации.

Это же задание выполнить с помощью ИС Eureka и Scilab.

 

ЗАДАНИЕ 7

 

Методом дихотомии и методом золотого сечения найти локальный минимум функции с погрешностью e < 0.12

a) y=0.05(m+q)x4–(3+0.5m)x3+(6+0.4n)x2– bx+q

b) y=0.1(a+m)x3–(2+n)x2+ 0.1(1+g)x– m–1

c) y=(a+2)·sin(0.3(n+1)x+b)+0.2gx·cos((m+1)x+q)

d) y=0.3(1+a)x/(x2 +bx +0.5)–2(g+1)/(x2+0.4 x+5)

Это же задание выполнить с помощью ИС Eureka и Scilab.

 


⇐ Предыдущая12
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.