
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача1.. Задача 2.. Задача 3.
Задача1.
В правильной треугольной призме АВСА 1В 1С1 все ребра которой равны 1, найти косинус угла между прямыми АВ и В 1С.
Решение
 1) Введем систему координат как на рисунке.
1) Введем систему координат как на рисунке.
2)Координаты 
 (
( 
3)  =
=  =
=  .
.
Ответ:  =
=  .
.
Задача 2.
В правильной четырехугольной пирамиде , все ребра которой равны 1, найти косинус угла между прямой АС и плоскостью АSД.
Решение
1) Введем систему координат как на рисунке.
Координаты  ( -1; 1; 0).Найдем координаты вектора нормали
( -1; 1; 0).Найдем координаты вектора нормали  ( х; у; z) к плоскости АSД. Для этого выберем в плоскости АSД два непараллельных вектора
( х; у; z) к плоскости АSД. Для этого выберем в плоскости АSД два непараллельных вектора  .
.
 Координаты векторов
Координаты векторов 


 *
*  и
и 
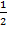 х -
х - 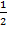 у -
у -  =0,
=0,
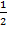 х
х  =0, при z =1, х=
=0, при z =1, х=  у =0.И так ,
у =0.И так , 
 АSД)) =
АSД)) =  =
=  =
= 
 .
. 
Задача 3.
В кубе АВСДА1В1С1Д1 точки Е и F – середины ребер соответственно А1В1 и А1Д1. Найдите косинус угла между плоскостями АЕF и ВДД1.
Решение

. Плоскость ВДД1 – это диагональное сечение куба. Вектор  перпендикулярен этой плоскости, поэтому
перпендикулярен этой плоскости, поэтому  – это вектор нормали к плоскости ВДД1.
– это вектор нормали к плоскости ВДД1.
А ( 0; 0; 0;), С(1; 1; 0) , тогда  =
=  1 ( 1; 1; 0).
1 ( 1; 1; 0).
2) Найдем вектор нормали  2(х; у; z) к плоскости АЕF. Выберем в этой плоскости два непараллельных вектора
2(х; у; z) к плоскости АЕF. Выберем в этой плоскости два непараллельных вектора 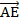 и
и 
3) Определим координаты векторов: А(0; 0; 0) , Е ( ½; 0; 1), F (0; ½; 1).
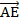 (1/2; 0; 1),
(1/2; 0; 1),  ( 0; ½; 1).
( 0; ½; 1).
4) Запишем скалярные произведения  2*
2* 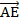 и
и  2 *
2 *  и приравняем их нулю
и приравняем их нулю
1/2х + 0у + z = 0, z = - 1/2х,
0х + ½ у + z = 0;  z = - 1/2у, при х = у =1, z = - ½.
z = - 1/2у, при х = у =1, z = - ½.
И так, вектор нормали  2( 1; 1 ; - ½)
2( 1; 1 ; - ½)
5) Найдем косинус угла между  1 и
1 и  2.
2.
| Cοs(АЕF,^ ВДД1) |= |cοs (  1,^
1,^  2)| =|
2)| =|  =
=  .
.
Ответ: cοsϕ = 
Задача 4: Доказать, что угол между скрещивающимися прямыми, одна из которых содержит диагональ куба, а другая — диагональ грани куба, равен .
Решение: изобразим прямоугольную координатную плоскость так, чтобы координатные оси совпадали с рёбрами куба.
Обозначим буквами вершины куба, через которые проходят данные скрещивающиеся прямые. Найдём угол между прямыми .
Пусть длина единичных отрезков на осях равна длине ребра куба.
Тогда в такой системе координат нетрудно найти координаты точек О, О1, О2 и О3.
А теперь найдём координаты векторов ОО1 и О2О3, которые являются направляющими для данных прямых.
Вектор . А вектор .
Найдём косинус угла между данными прямыми, подставив в формулу координаты направляющих векторов.
В ходе вычислений получаем, что
А значит, угол между прямыми .
Что и требовалось доказать.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|