Векторно-координатный метод решения задач

«Векторно-координатный метод решения задач

в стереометрии»

Цель урока:

рассмотреть векторно-координатный метод с применением скалярного произведения векторов для решения задач на нахождение углов

Координаты вершин кубав прямоугольной системе координат в пространстве со стороной равной единице:

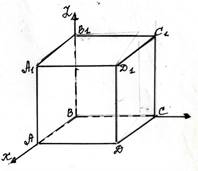А(1;0;0),В(0;0;0) , С(0;1;0),Д(1;1;0),А₁(1;0;1),В₁(0;0;1), С₁(0;1;1), Д₁(1;1;1) .

Координаты треугольной призмы в прямоугольной системе координат в

пространстве со стороной равной единице:

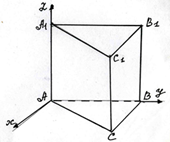А( 0;0;0) , В ( 0; 1; 0), С ( 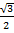; ; 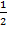0), А₁( 0; 0; 1), В₁(0; 1; 1),С₁(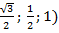

Координаты четырехугольной пирамиды в прямоугольной системе координат в пространстве со стороной основания ,равной единице:

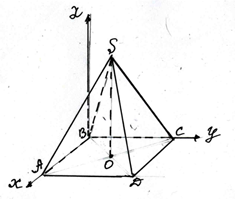А(1; 0; 0),В(0;0;0), С(0;1;0),Д(1;1;0), S(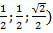

Алгоритм решения задач на нахождение угла между скрещивающимися прямыми векторно-координатным методом:

Угол между скрещивающимися прямыми заменяем углом между направляющими векторами этих прямых , который можно вычислить по теореме о скалярном произведение векторов по формуле:

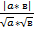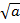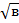Cos φ = , где |a * в| – модуль скалярного произведения векторов , а и – длины этих векторов.

Алгоритм решения задач на нахождение угла между прямой и плоскостью векторно-координатным методом:

Угол между прямой и плоскостью вычисляется по формуле

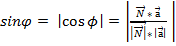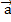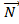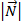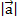, где – направляющий вектор прямой, - вектор нормали к плоскости, а и – длины этих векторов.

Вектор нормали к плоскости находим из условия его перпендикулярности двум непараллельным векторам плоскости. Чтобы найти координаты вектора нормали необходимо рассмотреть два скалярных произведения и приравнять их нулю.

Алгоритм решения задач на нахождение угла между плоскостями векторно- координатным методом:

Углом между плоскостями считают угол между векторами нормали к плоскостям , который можно вычислить по формуле

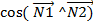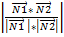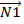= , где и 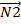–векторы нормали к плоскостям, а

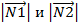– длины этих векторов

12 Следующая ⇒