Хелпикс

Главная

Контакты

Случайная статья



Тригонометрические функции - тангенс и котангенс.

⇐ ПредыдущаяСтр 2 из 2


Тригонометрические функции - тангенс и котангенс.

1. Функция у = tgх

Остановимся на графиках функций тангенса и котангенса. Сначала обсудим построение графика функции у = tg х на промежутке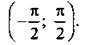

 

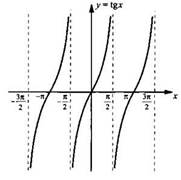
Учитывая периодичность функции тангенса, получаем ее график на всей области определения параллельными переносами вдоль оси абсцисс (вправо и влево) уже построенного графика на π, 2π и т. д. График функции тангенса называют тангенсоидой.

 Основные свойства функции у = tg х:

1. Область определения - множество всех действительных чисел, за исключением чисел вида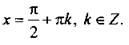

2. Функция нечетная (т. е. у(-х) = -y(x)), и ее график симметричен относительно начала координат.

3. Функция возрастает на промежутках вида 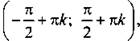где к ∈ Z.

4. Функция неограничена.

5. Функция не имеет наименьшего и наибольшего значений.

6. Функция непрерывная.7. Область значений Е(у) = (-∞; +∞).

8. Функция периодическая с наименьшим положительным периодом Т = π, т. е. у(х + пk) = у(х).

Домашнее задание

Постройте график функции

у = 2cos x -1

у = - cos 2x +1

у = tg х -3

Как получить график функции у = cos x, используя график функции у = sin х:

 


⇐ Предыдущая12
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.