ПРИЛОЖЕНИЕ A. ПРИЛОЖЕНИЕ Б. ПРИЛОЖЕНИЕ В. ЛИТЕРАТУРА

ПРИЛОЖЕНИЕ A

Нормированная функция Лапласа (в значениях функции ноль целых опущен, указаны только знаки после запятой).

														Таблица А.1

z

0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9

1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9

2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9

3 49865 49869 49874 49878 49882 49886 49889 49893 49896 49900

3,1 49903 49906 49910 49913 49916 49918 49921 49924 49926 49929

z
3,2 49931
3,3 49952
3,4 49966
3,5 49977
3,6 49984
3,7 49989
3,8 49993
3,9 49995

ПРИЛОЖЕНИЕ Б

Значения чисел q в зависимости от объёма выборки n и надёжности g для определения доверительного интервала среднего квадратического отклонения _.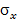

	g					g
n	0.95	0.99	0.999	n	0.95	0.99	0.999
	0.92	-	-		0.32	0.49	0.73
	0.80	-	-		0.28	0.43	0.63
	0.71	-	-		0.26	0.38	0.56
	0.65	-	-		0.24	0.35	0.50
	0.59	0.98	-		0.22	0.32	0.46
	0.55	0.90	-		0.21	0.30	0.43
	0.52	0.83	-		0.188	0.269	0.38
	0.48	0.78	-		0.174	0.245	0.34
	0.46	0.73	-		0.161	0.226	0.31
	0.44	0.70	-		0.151	0.211	0.29
	0.42	0.66	-		0.143	0.198	0.27
	0.40	0.63	0.96		0.115	0.160	0.211
	0.39	0.60	0.92		0.099	0.136	0.185
	0.37	0.58	0.88		0.089	0.120	0.162

ПРИЛОЖЕНИЕ В

		Критические точки распределения

Число	Уровень значимости a
степеней
степеней	0,01		0,05	0,1	0,90	0,95	0,99
свободы	0,01		0,05	0,1	0,90	0,95	0,99
свободы

	6,6		3,8	2,71	0,02	0,004	0,0002
	9,2			4,61	0,21	0,1	0,02
	11,3		7,8	6,25	0,58	0,35	0,12
	13,3		9,5	7,78	1,06	0,71	0,3
	15,1		11,1	9,24	1,61	1,15	0,55
	16,8		12,6	10,6	2,2	1,64	0,87
	18,5		14,1		2,83	2,17	1,24
	20,1		15,5	13,4	3,49	2,73	1,65
	21,7		16,9	14,7	4,17	3,33	2,09
	23,2		18,3		4,87	3,94	2,56
	24,7		19,7	17,3	5,58	4,57	3,05
	26,2			18,5	6,3	5,23	3,57
	27,7		22,4	19,8	7,04	5,89	4,11
	29,1		23,7	21,1	7,79	6,57	4,66
	30,6			22,3	8,55	7,26	5,23
			26,3	23,5	9,31	7,96	5,81
	33,4		27,6	24,8	10,1	8,67	6,41
	34,8		28,9		10,9	9,39	7,01
	36,2		30,1	27,2	11,7	10,1	7,63
	37,6		31,4	28,4	12,4	10,9	8,26
	38,9		32,7	29,6	13,2	11,6	8,9
	40,3		33,9	30,8		12,3	9,54
	41,6		35,2		14,8	13,1	10,2
			36,4	33,2	15,7	13,8	10,9
	44,3		37,7	34,4	16,5	14,6	11,5
	45,6		38,9	35,6	17,3	15,4	12,2
			40,1	36,7	18,1	16,2	12,9
	48,3		41,3	37,9	18,9	16,9	13,6
	49,6		42,6	39,1	19,8	17,7	14,3
	50,9		43,8	40,3	20,6	18,5

ЛИТЕРАТУРА

1. Гмурман, В. Е. Теория вероятностей и математическая статистика. Высшая школа / В.Е. Гмурман – М. : Высшее образование, 2008. – 479 с.

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. Высшая школа / В.Е. Гмурман – М. : Высшее образование, 2008. – 404 с.

3. Вентцель, Е.С. Теория вероятностей и ее инженерные приложения / Е. С. Вентцель, Л.А. Овчаров – М.: Издательский центр «Академия», 2003. – 464 с.

4. Тѐрушкина, О. Б. Математическая статистика. Методические указания и контрольные задания для студентов 2-го курса по направлениям подготовки: 036000.62 - Интеллектуальные системы в гуманитарной сфере; 090900.62 - Информационная безопасность – СПб: СПбГУПТД, 2014. – 34 с.

5. ГОСТ 7.32-2017 СИБИД. Отчет о научно-исследовательской работе. Структура и правила оформления. – Взамен ГОСТ 7.32-2001 ; Введ. 2018-07-01. – Москва: Стандартинформ, 2017. – 27 с.

⇐ Предыдущая 1 23