Содержание. ЗАКЛЮЧЕНИЕ

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Содержание

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. 5

ПРАКТИЧЕСКАЯ ЧАСТЬ. 7

Часть 1. 7

Часть 2. 16

ПРИЛОЖЕНИЕ A.. 20

ПРИЛОЖЕНИЕ Б. 22

ПРИЛОЖЕНИЕ В.. 23

СПИСОК ИСТОЧНИКОВ.. 24

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Генеральная совокупность - всё множество значений случайной величины Х.

Выборка - часть объектов из генеральной совокупности, отобранных для изучения, с целью получения информации обо всей генеральной совокупности. Число объектов, составляющих выборочную совокупность, называется объемом выборки.

Релевантность - соответствие генеральной совокупности.

Репрезентативность - соответствие характеристик выборки характеристикам генеральной совокупности в целом.

Ранжирование – это определение порядка элементов по их значению. Для таблицы данных доступно ранжирование по возрастанию и по убыванию. Ранжирование может применяться по строкам, по столбцам и по всей таблице.

Частота - число повторений определенного значения параметра в выборке.

Относительная частота – это отношение частоты к общему числу данных в ряду.

Несмещенная оценка - выборочный показатель, который при многократном повторении выборки стремится к своему теоретическому значению.

Доверительный интервал – интервал, который покрывает неизвестный параметр с заданной надёжностью.

Надёжность – это доверительная вероятность, с которой значения могут появиться в данном диапазоне

Дискретный вариационный ряд показывает каким образом числовые значения изучаемого признака связаны с их повторяемостью в выборке

Выравнивающие - частоты, найденные теоретически чем ближе друг к другу выравнивающие и эмпирические частоты, тем вероятнее нормально распределение.

Корреляция – статистическая взаимосвязь двух или более случайных величин. При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.

Регрессия - статистическая зависимость среднего значения случайной величины от значений другой случайной величины или нескольких случайных величин

ВОПРОС:

Почему в лабораторной оцениваем соответствие нормальному распределению непрерывной случайной величины, хотя обрабатываем дискретные данные?

При N = 20 в «многоугольнике» биноминального распределения уже просматривается нормальная кривая. Чем больше будет N, тем ближе будет сходство. И именно этот факт используется в теоремах Лапласа.

Поэтому биноминальное распределение случайной величины частот значений, полученных в испытаниях, очень близко к нормальному.

ПРАКТИЧЕСКАЯ ЧАСТЬ

Часть 1

Получены статистические данные (N = 20) зависимости результатов измерения массы фолклендских лисиц и длины их хвоста. Фолклендская лисица, или варрах, или фолклендский волк — единственное наземное млекопитающее Фолклендских островов.

Переменные: х – масса, у – длина хвоста.

Цель: определить - подчинена ли случайная величина Х (масса фолклендской лисицы) нормальному закону распределения. Для статистической проверки гипотезы необходимо построить эмпирическую функцию распределения, полигон, гистограмму для исследуемой случайной величины Х и затем построить течечные и интервальные оценки математического ожидания и дисперсии генеральной совокупности Х.

Исходная выборка представлена в Таблице 1.

Дата	Окт-14	Окт-15	Окт-16	Окт-17	Окт-18	Окт-19	Окт-20	Окт-21	Окт-22	Ноя-2
i
X	4,0	4,0	4,0	3,4	3,5	4,1	4,1	4,3	4,3	3,7
Y	24,2	25,2	23,1	21,8	23,3	32,2	27,3	25,7	24,8

Дата	Окт-23	Окт-24	Окт-25	Окт-26	Окт-27	Окт-28	Окт-29	Окт-30	Окт-31	Ноя-1
i
X	4,4	3,6	3,6	3,9	3,2	3,0	3,1	3,0	2,7	2,8
Y	25,1	23,5	24,9		20,5	19,4			18,9

За X взято количество инцидентов заражения в России в миллионах. За Y – количество уязвимостей в тысячах.

Данные за октябрь-ноябрь 2020 года.

https://cybermap.kaspersky.com/ru/stats#country=213&type=vul&period=m

Составим ранжированный (по увеличению X) ряд для случайных величин X, Y.

ТАБЛИЦА 2. Ранжированный ряд случайной величины Х

ТАБЛИЦА 3.Дискретный вариационный ряд

Cоставим таблицу, в которой отразим частоты n_i появления случайных величин X_i(n_i – столько раз данный X_iпоявляется в выборке), и относительные частоты p_i=n_i/N (Напомним N – объём выборки, в нашем случае N=20).

В данном примере случайные величины X находятся в интервале [2,7;4,4] включая границы.

Интервал варьирования R («размах») будет равен R = 4,4 – 2,7 = 1,7;

Длину интервала рассчитывают по формуле (появление lg и множителя 3,28 выходит за рамки курса):

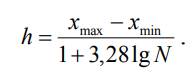
Подставляем значения и получаем:

h = 0,3227

Округлим до 0,3

h = 0,3

Тогда чисто интервалов будет равно 6;

Соответствующий интервальный вариационный ряд для 6 интервалов приведён в табл. 4.

ТАБЛИЦА 4.Интервальный вариационный ряд

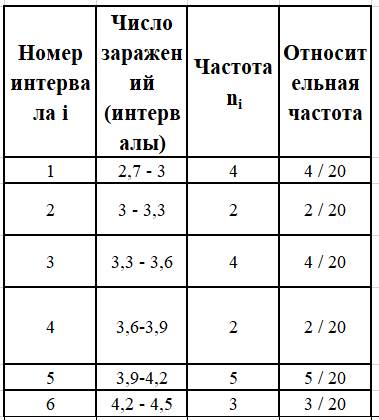
Контрольные суммы (промежуточный контроль ) ∑ n_i = 20 ;

∑ p_i = 20/20 = 1;

После составления вариационного ряда необходимо построить функцию распределения выборки или эмпирическую функцию F*(x)= n_x / N, то есть функцию найденную опытным путём. Здесь n_x– относительная частота события Х< х, N - общее число значений.

ТАБЛИЦА 5.Расчёт эмпирической функции распределения

На основании полученных выборочных данных необходимо сделать предположение, что изучаемая величина распределена по некоторому определённому закону. Для того чтобы проверить, согласуется ли это предположение с данными наблюдений, вычисляют частоты полученных в наблюдениях значений, т.е. находят теоретически сколько раз величина Х должна была принять каждое из наблюдавшихся значений, если она распределена по предполагаемому закону. Для этого находят выравнивающие (теоретические) частоты по формуле:

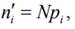
где N – число испытаний, p_i - вероятность наблюдаемого значения x_i, вычисленная при допущении, что Х имеет предполагаемое распределение.

ТАБЛИЦА 6.Дискретный вариационный ряд

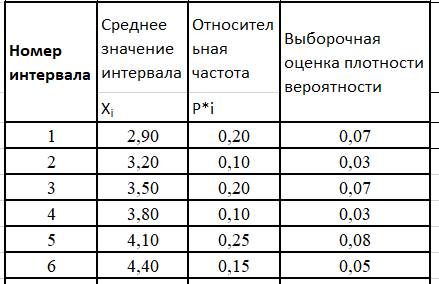
Рис. 1.Эмпирическая функция распределения

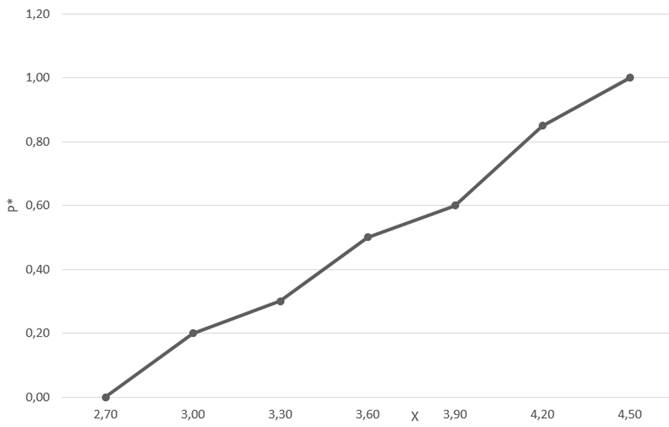
Эмпирические (полученные из таблицы, сплошная линия на рис. 2) и полученные позже выравнивающие частоты сравнивают, и при небольшом расхождении данных делают заключение о выбранном законе распределения. Мы предположим, что случайная величина Х распределена нормально (в случае, когда на случайную величину влияют многие различные причины, действие некоторых из них мы часто не в состоянии описать, это наиболее часто встречающееся распределение). В этом случае выравнивающие частоты находят по формуле:

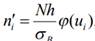
где N-число испытаний, h-длина частичного интервала, 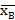, s_B -выборочное среднее и выборочное среднее квадратичное отклонение соответственно

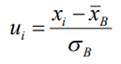
(x_i - середина i – го частичного интервала),

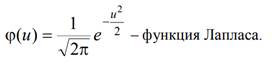
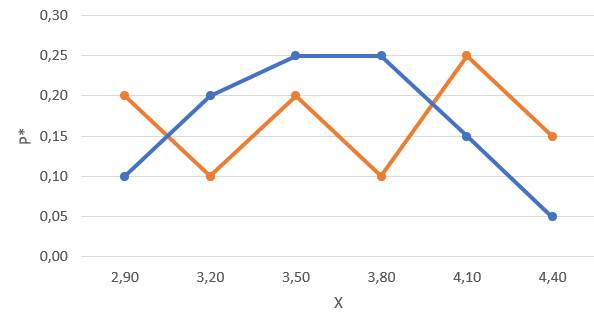
Результаты вычислений отобразим в табл. 7. Сравнение графиков (рис. 2) наглядно показывает близость выравнивающих частот к наблюдавшимся и подтверждает правильность допущения о том, что обследуемый признак распределён нормально. Напомним, что теоретические частоты будут рассчитаны ниже.

Рис. 2.Эмпирические и теоретические частоты

Интервальный вариационный ряд графически изобразим в виде гистограммы (рис. 3). На оси Х отложим интервалы длиной h=2, а на оси Y значения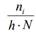

расчёт которых представлен в табл. 6. Площадь под гистограммой равна сумме всех относительных частот, т.е. единице. Графическое изображение вариационных рядов в виде полигона и гистограммы позволяет получать первоначальное представление о закономерностях, имеющих место в совокупности наблюдений. Найдём числовые характеристики вариационного ряда, используя табл.4.

Рис. 3.Гистограмма интегрального вариационного ряда

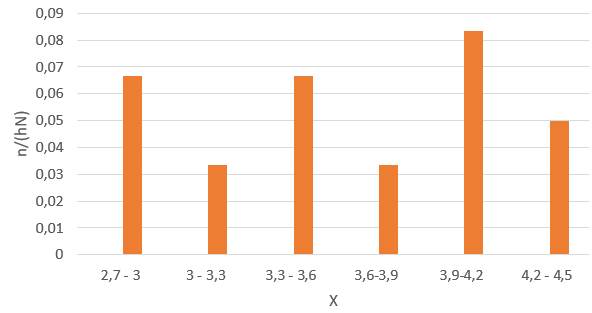
ТАБЛИЦА 7. Расчёт выравнивающих частот (с округлением ni ¢ , N n p i i ¢ = *¢ )

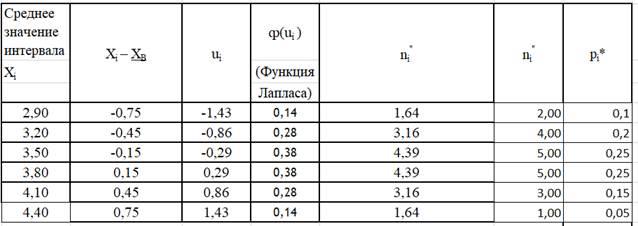
Среднеквадратическое отклонение

åni ¢ = 20;

- далее вычисляют вероятности попадания случайного числа в интервал с помощью (интегральной) функции распределения (напомним, что слово «интегральная» может быть опущено).

S= 0,29; X_B=3,65;

ТАБЛИЦА 8.Определение X2

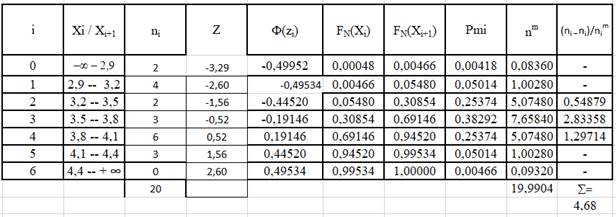
Результаты вычисления p_iт , n_iт , и c_r2 приведены в табл. 8.

Выберем уровень значимости α=0,05. Чем больше уровень значимости, тем строже критерий. По таблице приложения 3 можно найти число c²_r (критическое», т.е предельно допустимое для принятия основной гипотезы) для уровня значимости α=0,05 и числа степеней свободы l=k-3=10-3=7

кр

(напомним, k=10 – число интервалов, см. табл. 6) находим c²_кр = 13,98 .

Следовательно, критическая область - (14,1; ¥). Величина c_r2 = 13,98 не входит

в критическую область, поэтому гипотеза о том, что случайная величина Х подчинена нормальному закону распределения, не отвергается. Строго формулируя, «нет оснований отвергнуть основную гипотезу».

Индекс «r» означает сокращение от английского real, в нашей литературе часто вместо него пишут «набл.», т.е. реально наблюдаемое значение критерия.

Часть 2

Цель: Рассчитать коэффициент корреляции двух величин Х и Y, вывести соответствующие уравнения линейной регрессии и сделать анализ полученных величин.

Данные таблицы 3 сгруппируем в корреляционную таблицу 9 в виде корреляционной таблицы.

Таблица 9 – Корреляционная таблица

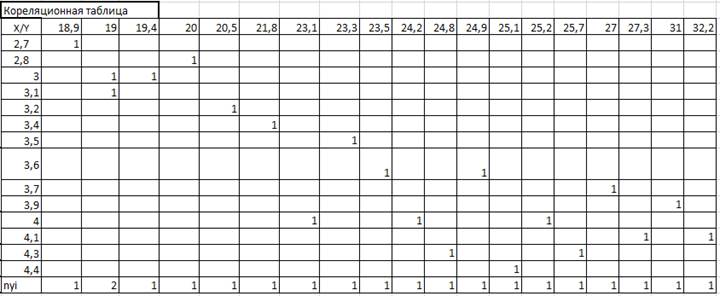
Строим в системе координат множество, состоящее из 20 экспериментальных точек (рис. 4). По расположению точек делаем заключение о том, что экономико-математическую модель можно искать в виде y = kx + b.

Рис. 4 – Экспериментальные точки

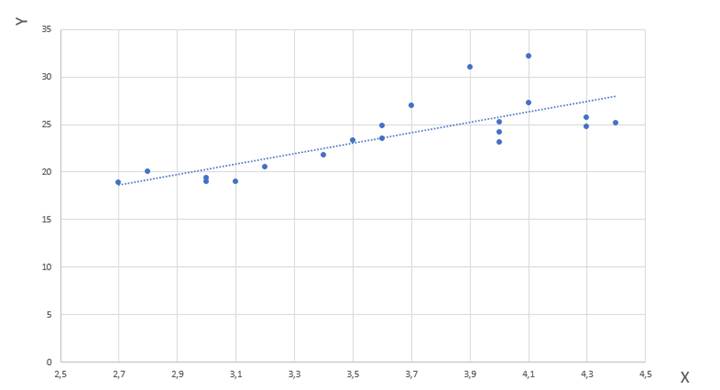
Найдём выборочные уравнения линейной регрессии. Для упрощения расчётов разобьём случайные величины Y на интервалы и выберем средние значения. Для величины Х указанные действия были выполнены в 1-й части задания.

Для случайной величины Y, используя формулу 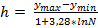, h = (32,2-18,9)/(1+3,28ln20) = 13,3/10,83 = 1,23, округляя получим h=1, число интервалов равно 14, т.к. интервал варьирования(размах) равен 13,3 (округленно 14), соответственно нам нужно 14 интервалами по 1, закрыть 14 единиц, что не меньше нашего 13,3. Результаты внесём в таблицу 10 со сгруппированными данными.

Таблица 10 – Сгруппированные данные выборки

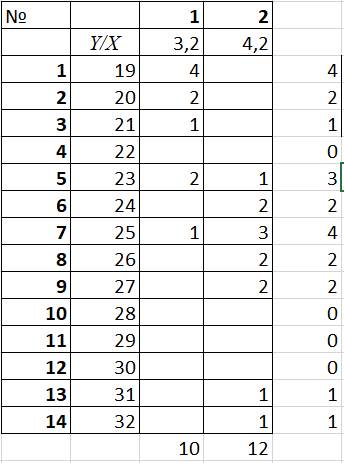
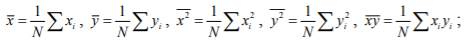
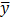= 24,04 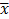=3,55 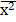=12,87 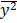=591,43

xy = 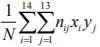=(18,9 × 2,7 + 19 × 3 + 19 × 3,1 + 19,4 × 3 + 20 × 2,8 + 20,5 × 3,2 + 21,8 × 3,4 + 23,1 × 4 + 23,3 × 3,5 + 23,5 × 3,6 + 24,2 × 4 + 24,8 × 4,3 + 24,9 × 3,6 + 25,1 × 4,4 + 25,2 × 4 + 25,7 × 4,3 + 27 × 3,7 + 27,3 × 4,1 + 31 × 3,9 + 32,2 × 4,1) / 20 =

=87,949

Используя формулы:

s xB = 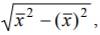, s yB = 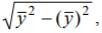, получим

s _{xB =}0.517, s _yB =3.675

4) Вычисляем выборочный коэффициент корреляции rB по формуле

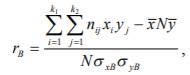
rB = (87,9 -24,04*3,6) / (0,517*3,675)=0.6461989349154765 ~ 0.6

Принято считать, что если 0,1<│r_В│<0,3 – связь слабая, если 0,3<│r_В│<0,5 – связь умеренная, если 0,5<│r_В│<0,7 – связь заметная, если 0,7<│r_В│<0,9 – связь высокая (тесная), если 0,9<│r_В│<0,99 – связь весьма высокая (весьма тесная). │r_В=1│ – существует линейная функциональная зависимость, одна величина есть линейная функция другой. Если при этом r_В>0, то с увеличением X растёт и Y, r_В<0 – с ростом X - Y уменьшается.

Для данного примера связь между X и Y умеренная, с ростом X Y «немного» растёт.

Составим выборочное уравнение линейной регрессии Y на X в виде

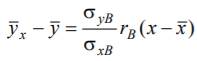
и выборочное уравнение линейной регрессии X на Y;

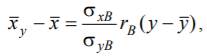
x_y - 3,55 =0,517*0,6/3,675(y – 24,04)

или

xy = 0,08y + 1,52

yx - 24,04 =3,675*0,6 / 0,517(x –3,55)

или

yx = 4,2x + 8,9.

Обратите внимание, что из уравнения регрессии Y на X нельзя получить уравнение регрессии X на Y просто выразив X через Y.

ЗАКЛЮЧЕНИЕ

Модуль выборочного коэффициента корреляции принадлежит интервалу от 0,5 до 0,7 (если 0,5<│r_В│<0,7), что говорит о том, связь между случайными величинами X и Y заметная. А положительный выборочный коэффициент корреляции (rB > 0), говорит о том, что вместе с увеличением X растёт и Y. Выборочное уравнение линейной регрессии X на Y:

xy= 0,08y + 1,52 ,

Выборочное уравнение линейной регрессии Y на X:

yx  4,2x +8,9.

Заметная корреляция показывает нам, что количество найденных уязвимостей и количество инцидентов заражения умеренно связано. Действительно, при обнаружении новых CVE злоумышленники эксплуатируют найденную ими, или опубликованную новую уязвимость. Отсюда и появился термин -Угроза нулевого дня. Когда разработчик программного обеспечения выпускает решение с брешью, о которой еще не известно ни ему самому, ни производителям антивирусных решений, ее называют уязвимостью или мишенью для атаки нулевого дня.

После проделанной статистической работы с данными, можно сделать вывод о том, что каждый раз, когда находятся новые уязвимости, то в ускоренном порядке надо задействовать штат сотрудников по информационной безопасности. Пренебрежение такой закономерности между новыми CVE и заражающими эксплойтами может принести ущерб не только финансовый, но и репутационный. Незакрытые уязвимости, "дыры" и ошибки на узлах сетевой инфраструктуры компании дают злоумышленникам немало возможностей. Одна неисправленная ошибка способна привести приостановке деятельности компании и штрафам со стороны регуляторов. Для аудита безопасности важно использовать сервисы контроля уязвимостей, с помощью которых заказчики могут сканировать как внешний периметр организации, так и внутреннюю сеть (веб-приложения, серверы, сетевые устройства, рабочие места (в том числе удалённых сотрудников – с помощью агентских модулей).

Анализ уязвимостей информационной системы является одним из наиболее важных мероприятий, как при аттестации информационной системы, так и при текущем контроле защищенности. Для осуществления такой процедуры необходимо использовать сертифицированные сканеры. Для организаций, которые не желают приобретать такой продукт, анализ уязвимостей может быть оказан как периодическая услуга.

Результатом анализа уязвимостей при определенных обстоятельствах может стать огромный документ объемом 100 и более и страниц. Важность анализа уязвимостей заключается не столько в самом сканировании системы, сколько в последующем анализе отчета о найденных уязвимостей и в адекватном реагировании на выявленные уязвимости.

Данная статистическая работа была нацелена поднять вопрос о важности аудита безопасности для любой компании использующую информационные системы.

⇐ Предыдущая 123 Следующая ⇒