
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Таблица 3. Интервальный и соответствующий ему дискретный вариационный ряд частот для выборочных данных
Таблица 3. Интервальный и соответствующий ему дискретный вариационный ряд частот для выборочных данных
| Интервалы [ci-1, ci) | |||||||||
Середины
интервалов 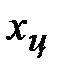
| |||||||||
Частоты 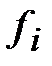
|
По полученному дискретному вариационному ряду частот вычисляем выборочную среднюю взвешенную 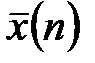 и общую дисперсию
и общую дисперсию 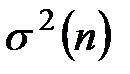 параметров распределения признака
параметров распределения признака 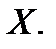
Выборочная средняя взвешенная 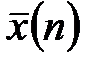 вычисляется по формуле:
вычисляется по формуле:
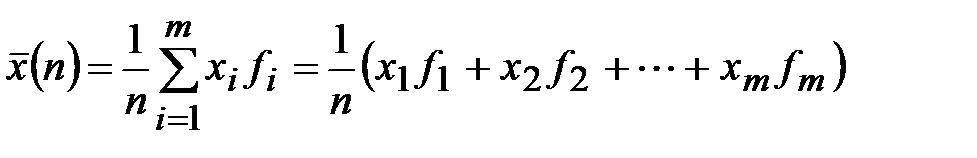 ,
,
где т равно числу интервалов. Для нашей задачи n = ____, т= _____. При этом рекомендуется (во избежание слишком больших погрешностей округлений) в результатах промежуточных вычислений брать на 2 знака после занятой больше, чем у исходных данных. Вычисляем:
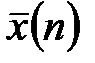 =
= 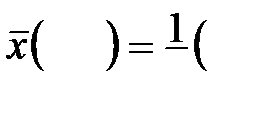
Обязательно следует поместить значение 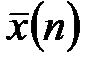 на ось абсцисс гистограммы (на рис1.). При этом следует помнить смысл математического ожидания и его оценки
на ось абсцисс гистограммы (на рис1.). При этом следует помнить смысл математического ожидания и его оценки 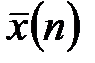 - это среднее взвешенное значений признака
- это среднее взвешенное значений признака  Посмотрите, является ли значение
Посмотрите, является ли значение 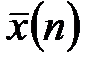 «центром тяжести» гистограммы? Если уже визуально это не подтверждается, то дальнейшие вычисления бессмысленны. Рекомендуется этот этап вычислений согласовать с преподавателем и только после этого продолжать вычисления.
«центром тяжести» гистограммы? Если уже визуально это не подтверждается, то дальнейшие вычисления бессмысленны. Рекомендуется этот этап вычислений согласовать с преподавателем и только после этого продолжать вычисления.
Проверим выборочную среднюю, используя для её расчётов метод моментов. Для этого Перепишем отдельно две нижние строки таблицы 3:
Таблица 4.
Середины
интервалов 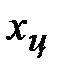
| |||||||||
Частоты 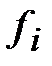
|
Моду 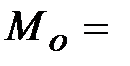 _________ этого дискретного ряда примем её за условный ноль.
_________ этого дискретного ряда примем её за условный ноль.
(Модой дискретного ряда называется _______________________________________________
_______________________________________________________________________________
Условные значения вариант будем вычислять, как их отклонения от условного ноля, делённые на шаг h = ________:
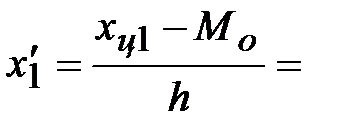
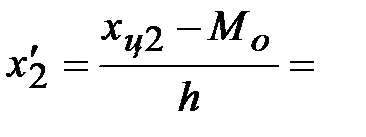
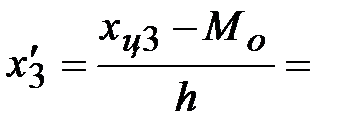
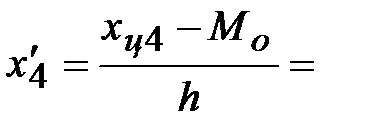
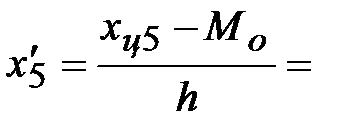
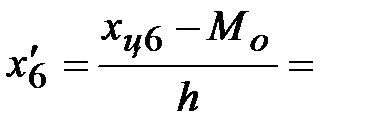
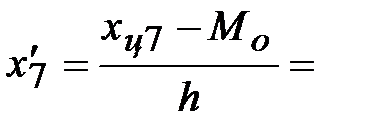
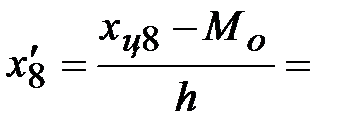
Тогда, средняя взвешенная для условных вариант будет равна:
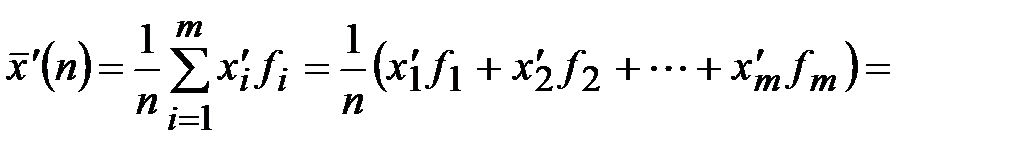
Окончательно среднюю взвешенную находим, как
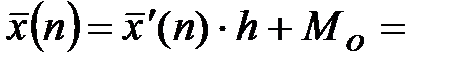
Выборочную общую дисперсию 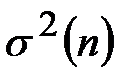 можно рассчитать по одной из двух формул:
можно рассчитать по одной из двух формул:
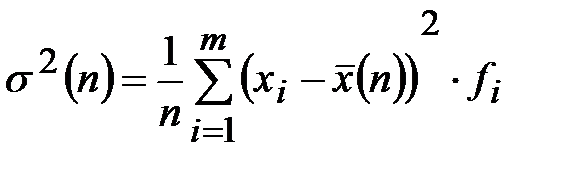 , (1)
, (1)
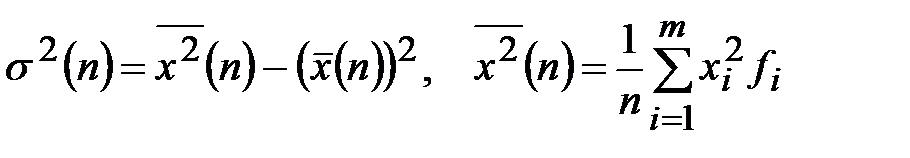 . (2)
. (2)
Рассчитаем выборочную дисперсию для нашей задачи по обеим формулам (1) и (2). Сначала рассчитываем по формуле (1):
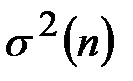 =
= 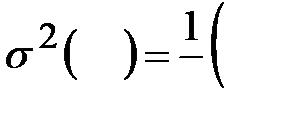
Теперь рассчитываем выборочную дисперсию по формуле (2), вычисляя предварительно средний квадрат:
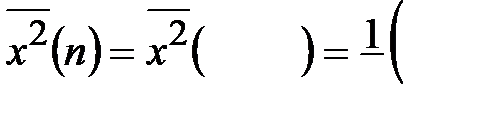
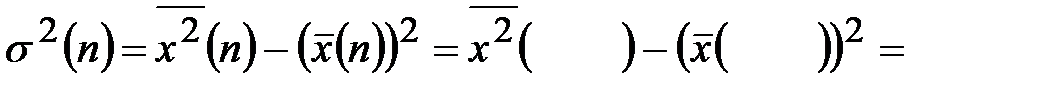
Видим, что результаты расчётов выборочной дисперсии по формулам (1) и (2) практически совпадают (возможное различие связано только с погрешностями вычислений). Итак, 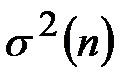 =
=  _______.
_______.
Для визуального контроля следует учитывать правило трех сигм нормального распределения, т.е практически вся гистограмма должна укладываться в окрестности  радиуса трех
радиуса трех  Проверьте это на рис.1.
Проверьте это на рис.1.
Итак,
выборочная средняя взвешенная 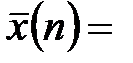 ________, общая дисперсия
________, общая дисперсия 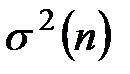 _________.
_________.
3. Будем считать наши исходные данные генеральной совокупностью и сделаем из неё способом собственно-случайного отбора выборку объёма n = 10.
Собственно-случайным отбором называют такой способ отбора, при котором ________________________________________________________________________________
________________________________________________________________________________________________________________________________________________________________
Итак, в выборку объёма n = 10 попали следующие значения:
По полученной малой выборке вычисляем выборочную среднюю 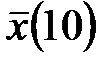 , выборочную общую дисперсию
, выборочную общую дисперсию 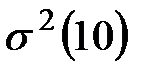 и среднюю ошибку выборки.
и среднюю ошибку выборки.
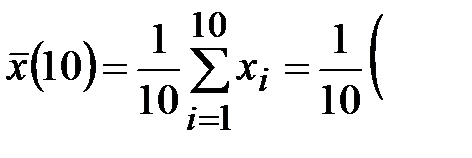
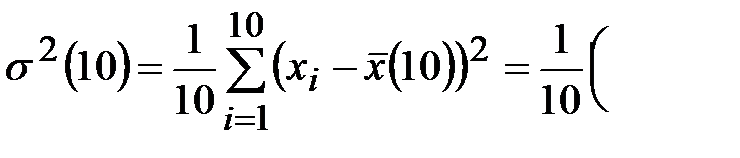
При случайном бесповторном отборе средняя ошибка выборки рассчитывается по формуле 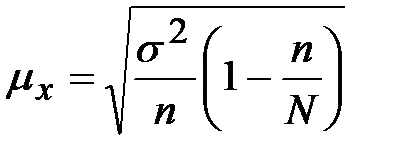 , где n –объём выборки, N - объём генеральной совокупности.
, где n –объём выборки, N - объём генеральной совокупности.
Тогда, 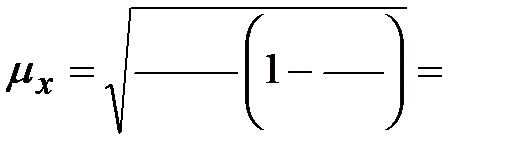
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|