Хелпикс

Главная

Контакты

Случайная статья



Институт подготовки государственных и муниципальных служащих

Стр 1 из 2Следующая ⇒


 

Федеральное казенное образовательное учреждение высшего

профессионального образования

"Академия права и управления Федеральной службы исполнения наказаний"

России

Институт подготовки государственных и муниципальных служащих

Академии ФСИН России

 

 

Кафедра математики и информационных технологий управления

 

РАБОЧАЯ ТЕТРАДЬ ДЛЯ ВЫПОЛНЕНИЯ РАСЧЁТНОЙ РАБОТЫ

ПО СТАТИСТИКЕ

 

Заполнил(а) студент(ка) ______ группы

  направления _______________________

___________________________________

(Ф.И.О.) ___________________________

Вариант № ____

 

Проверил преподаватель

 

__________________________________

 

 

Рязань ____________

Задание № 1. (на повторение дисциплины «Математическая статистика»)По выборке объёма n = ___ исследуется признак Х –  _____________________________________________

_______________________________________________________________________________.

Распределение признака подчинено нормальному закону. Выборочные данные помещены в таблицу 1.

 

ТРЕБУЕТСЯ:

1. Сгруппировать выборочные данные в интервальный вариационный ряд. Изобразить вариационный ряд графически, построив гистограмму частот.

2. Вычислить по сгруппированным данным выборочную среднюю взвешенную 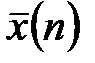, общую дисперсию .

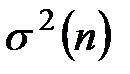3. Считая исходный набор данных генеральной совокупностью, сделать из неё способом собственно-случайного отбора выборку объёма n = 10, для которой вычислить среднюю 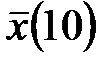, выборочную дисперсию  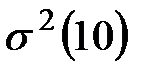и найти среднюю ошибку выборки.

Решение. Поместим исходные данные в таблицу 1:

 

Таблица 1.      Исходные выборочные данные для признака Х

                   
                   
                   
                   
                   
                   
                   
                   
                   
                   

 

1. Для признака Х по результатам выборки составляется интервальный вариационный ряд. Для этого весь диапазон изменения выборочных данных – размах вариации 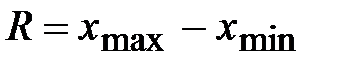 – накрывается совокупностью 5 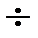8 полузамкнутых интервалов  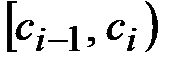или 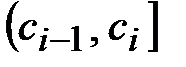,  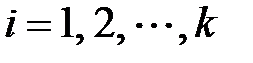одинаковой длины (шага) h так, чтобы значение  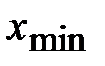находилось приблизительно посередине первого интервала, а значение  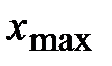находилось в последнем интервале. Эту длину рекомендуется вычислять, как 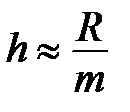,  где m – оптимальное число групп, определяемое по формуле Стерджеса: .

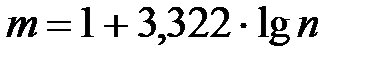h округляем до удобного для дальнейших вычислений. Значения десятичных логарифмов помещены в следующей таблице:

 

n
lg n 1,60 1,70 1,78 1,85 1,90 1,95 2,04 2,08

 

В нашей задаче 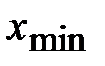=_______, 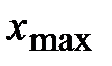=_______, n = _____, поэтому, округляя результат вычислений формулы Стерджеса, возьмём h = _____. Определяем левый конец первого интервала 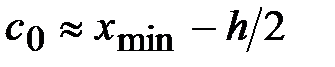= ________________________. Затем определяем границы остальных интервалов  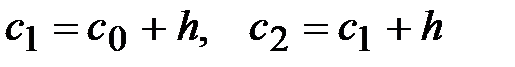и т.д., пока значение  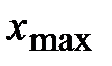не окажется в интервале с номером 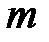, являющимся последним. Для разнесения данных из таблицы 1 по интервалам построим таблицу 2, в которой определим частоты  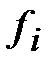попадания выборочных данных в интервалы (частота  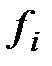- это число значений признака Х, попавших в интервал с номером 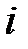). Получим интервальный вариационный ряд частот.

Таблица 2.  Разнесение выборочных данных по интервалам и подсчёт частот

Интервалы [ci-1, ci)                  
Частоты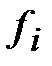                  

 

Контроль: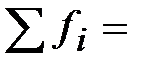

 

Количество интервалов оказалось равным т = ____. По таблице 2 следует осуществить контроль подсчёта частот: 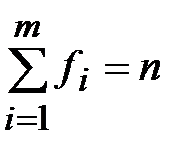, где n – объём выборки.

Если контроль оказался верным, переходим к следующим этапам работы, если же нет, то заполняем (исправляем) таблицу 2 повторно до выполнения контрольного равенства.

 

Графическим изображением интервального вариационного ряда, отражённого в таблице 2 служит гистограмма частот. Построим гистограмму частот на рисунке 1. Для этого на оси абсцисс откладываем отрезки, изображающие интервалы 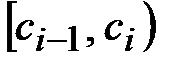 изменения значений х признака Х. На этих отрезках как на основаниях строим прямоугольники с высотами, равными частотам 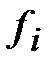. Полученная фигура и называется гистограммой частот.

 

 

 

                                                                                          

 

 


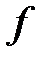
0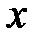                                                                                                 

 

Рис. 1. Гистограмма частот интервального вариационного ряда.

 

2. Вычислим теперь выборочную среднюю взвешенную 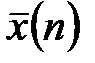 и общую дисперсию 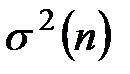. Для решения этой задачи используем Таблицу 2 и  вычислим середины интервалов 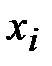, придав им соответствующие частоты  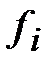из интервального вариационного ряда.

 

Вычисляем середины интервалов 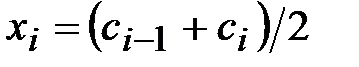, преобразуем таблицу 2 в таблицу 3, соединяя в ней интервальный вариационный ряд частот (первая и третья строки) и соответствующий ему дискретный вариационный ряд частот (вторая и третья строки).


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.