Вопрос 3. Дескриптивные модели

Вопрос 1. Модель-явление,предмет,установка,знаковое образование или условный образ(описание,схема)находящ-ся в некот.соответствии с изученным объектом и способное замещать его в процессе исслед-ия давая информ-ию об объекте.

Примеры:архитектор,здание нового типа, на компьютере или из кубиков,плакат на котор.изобр.система кровообращения

Применение:Хорошо построенная модель доступнее для исслед-ия,чем реальный объект. Некотор.объекты вообще не могут быть изучены непосредственным образом:недопустимые эксперименты с экономической страны в позн-ых целях,неосущ-ые эксперем.с прошлым или с планетами солн-ой системы. С помощью модели выявл-ся наиболее сущ-ые факторы,форм-ие те или иные св-ва объекта,т.к. сама модель отраж-ет лишь некот.харак-ки исходного объекта.

Классификация моделей:

1)Исследовательские(строят для изучения указанных характер-ик).

-эксперементальные (реально осуществл-ое устройство двух основных типов:

Тип1. Им.ту же природу,что и модел-ый объект,но воспроизв.его в опр-ом масштабе. Созд-ся на основе теории подобия. При этом подобие осущ-ся по тем параметрам,кот.существенны для изуч-ых характ-ик.

Например: Для эксперементального исследования сопротивления движению судна нужна можель,внешней формы кот. Подобна внеш.форме оригинала. А для иссл-ия прочности того же судна нужна модель,воспр-ая его силовой каркас.

Тип2. Основаны на встреч-ся совпадениях матем-го описания различных явлений.

Например: колеб-ые явления в механических и электрических сист-ах опис-ся одинаковыми дифер-ми урав-ями. Это позволяет вместо сложного эксперимента на мех-ой модели поставить более простой эксперимент на электр.моделе.

-Теоретические. Форм-ся на языке науки. В завис-ти от хар-ра этого языка говорят о матем-ой моделе,физической и экономич.

2) Рабочие.

(для непосредственного испол-ия)

Вопрос 2. Матем. М.-приближ-ое описание какого-либо класса явлений внеш.мира,выраж-ой с помощью матем.символики)

Математ.моделью служит:система ур-ий,фун-ия,матрица,геом-ий образ,вектор,число.

Для нескол.явлений модели с форм-ых позиций могут оказ-ся одинаковыми. В таких случаях матем.изучение их одинаково. С др.ст. для одного и того же явления можно создать не 1,а неск.разл.моделей,отр-их его с разн.сторон.

Принятие М.М. зависит от цели,пост-ой исслед-ем,от фактич-го уровня науки,от имеющ-ся ср-в изучения. При выборе нужной модели нужно руковод-ся:

1) Адекватность процессу

2) Разрешимость модели

Этапы М.М.:1) Исслед-ие задачи,построение предметной М.

2)Построение М.М.

3)Исслед. М.М.

4)Интерпритация результата

Вопрос 3. Дескриптивные модели

Дескриптивные (описательные) модели нужны

для того, чтобы описать происходящие процессы,

изучить их основные закономерности.

Различн.проц-ы биологии опис-ся дифер.урав-ем вида:
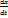=kx, при k < 0,это урав-ие явл.моделью радиоактивного распада, х-число нераспав-ся ядер к моменту времени t,

k- пост-ая радиоакт.распада.

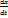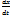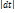-скорость распада, при k > 0,ур-ие явл-ся моделью развития популяций.В условиях неогран-ти ресурсов питания и отсутствия влияния др.видов. =kx /x, = kdt,

= kdt, ln 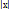=kt+C1,

Составить нужно модель динам.системы «хищник-жертва» и исслед-ть сост.этой сист-ы. Решение: Популяция жертвы может сущ-ть сама по себе,а попул.хищ-ка,только питаясь ей. В отсутствии хищника жертва размн-ся по 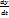=сy, где с-коэф.прироста жертвы.

Хищник в отсут-ии жертвы вымирает:

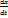= - ax, где (-a)-коэф.вымирания хищника,постоян.,отриц.

Хищник съедает тем более жертвы,чем её больше и чем более многочисленен он сам,поэтому при наличии хищника

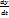=сy-dxy. Съеденное кол-во жертвы способствует размн-ию хищника и 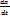= - ax+bxy.

Вопрос 4. Оптимизационные модели(улучшающие) Целенаправленная деятельность предполагает, как правило, достижение наилучшего результата, т.е. в зависимости от целей управления необходимо найти такие значения переменных управления, при кот.достигается либо мах значение,либо мin значение.

Вопрос 5. Все зад-и лин-го прогр-ия можно разделить на

След.группы: *Зад-и об испол-ии сырья,ресурсов,планир-ия производства

*Зад-и составл-ия рациона

*Зад-и об испол-ии мощностей,загрузке оборудования

*Транспортные зад-и.

Задача об использовании ресурсов.

Виды продукции: Р1 и Р2, Типы ресурсов: S1,S2,S3,S4.

Запасы ресурсов,число единиц ресурсов, затрач-ых на изготовление ед. продукции преведены в таблице.

Прибыль,получ-ая от ед.продукции Р1 и Р2, соот-но 2 и 3 ден.ед, необходимо составить план производства прод-ии,при кот.прибыль от её реализации будет максимальной.

вид ресурса	Запас ресурса	Число ед ресурсов,затрачив-ых на изготовление единицы продукции
вид ресурса	Запас ресурса	Р1	Р2
S1
S2
S3		-
S4			-

Решение: Х1 и Х2-число ед.продукции Р1 и Р2 заплан-ых к произ-ву.

F(х)=2х1+3х2 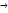мах

1х1+3х2≤18, 2х1+х2≤16, х2≤5, 3х1≤21.

Х1≥0, х2≥0.

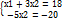
Х2=4, Х1=6. Ответ: Fмах=F(6,4)=2*6+3*4=24 ден. ед.

Вопрос 6. Все зад-и лин-го прогр-ия можно разделить на

След.группы: *Зад-и об испол-ии сырья,ресурсов,планир-ия производства

*Зад-и составл-ия рациона

*Зад-и об испол-ии мощностей,загрузке оборудования

*Транспортные зад-и. Составление рациона.

Им. 2 вида корма,сод-ие пит.вещ-ва │ и ║

(витамины S1,S2,S3). Сод-ие числа единиц пит-ых вещ-в в 1 кг каждого вида корма и необходимый min пит-ых вещ-в приведены в таблице. Стоим.1 кг корма │ и ║ соотв-но= 4 и 6 ден.ед.

Нужно составить дневной рацион, им-ий min стоимость,в кот.сод-ие кажд.вида пит.вещ-в было бы не менее устан-го предела.

Пит.вещ-во вит-ны	Необходим. Min пит.веществ	Число ед. пит. веществ в 1 кг корма
		│	║
S1
S2
S3

Решение: х1 и х2-кол-во кормов │ и ║, вход-их в дн-ой рацион. F(х)=4х1+6х2→min

3х1+х2≥9, х1+2х2≥8, х1+6х2≥12, х1≥0, х2≥0.

График тут по Уравнениям и их табличкам!

Х2АВСDХ1-обл.допустимых планов.

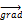F (4,6). т.В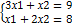

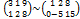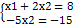
х2=3,х1=2. Fmin =F(2,3)=4*2+3*6=26 ден.ед.

Вопрос 7. Линейное программирование — решение линейных уравнений (уравнений первой степени) посредством составления программ и ‑
применения различных методов их последовательного решения, существенно облегчающих расчеты и достижение искомых результатов.
Условия задачи на оптимум и цель, которая должна быть достигнута, могут быть выражены с помощью системы линейных уравнений. Поскольку уравнений меньше, чем неизвестных, задача обычно имеет не одно, а множество решений. Найти же нужно одно, согласно терминологии математиков, экстремальное решение.

Линейное програмирование.

Найти: наиб.(наим)значение ф-ии F(х)=С1Х1+С2Х2+…+СnXn→ max(min) при ограничениях:

A11X1+A12X2+…+A1nXn≤B1,

A21X1+A22X2+…+A2nXn≤B2,

Am1X1+Am2X2+…+AmnXn≤Bm,

Am+1,1X1+Am+1,2X2+…+Am+1,nXn=Bm+1,

Am+p,1X1+Am+p,2X2+…+Am+p,n Xn=Bm+p и усл.неотриц-ти. Хi≥0, i=1,2,…,n. Если сод-ит только равенства,то задача явл.канонического вида. Если сод-ит только неравенства,то зад.-стандартного вида,

Если сод-ит и то,и то-зад.общего вида.

Вопрос 9. Линейное программирование — решение линейных уравнений (уравнений первой степени) посредством составления программ и ‑
применения различных методов их последовательного решения, существенно облегчающих расчеты и достижение искомых результатов.
Условия задачи на оптимум и цель, которая должна быть достигнута, могут быть выражены с помощью системы линейных уравнений. Поскольку уравнений меньше, чем неизвестных, задача обычно имеет не одно, а множество решений. Найти же нужно одно, согласно терминологии математиков, экстремальное решение.

Симплексный метод.

На первом шаге за основные переменные берут дополнительные перем-ые.

Т.к. в F(х) коэф-ы перед х1 и х2 пол-ые,то знач-ие фун-ии можно увел-ть переведя х1 и х2 в осн.пер. Оценка роста неосновной переменной:

Хi-перевод-ая неосн-ая переем-ая, Bj-своб.член,

Аij-коэф. при Хi

Ур-ие Хj=Вj+…АijXi+… опред-ет наиболее возм-ое зн-ие Хi по следующ. правилам: 1)Хi= 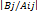,если Bj и Aij разн.знака, 2) Хj=∞,если Bj и Aij одного знака. 3) Xi=0,если Bj=0, а Аij<0. 4) Xi=∞,если Вj=0, Аij>0, 5) Xi=∞,если Aij=0.

Вопрос 12. Симплексный метод.

Для решения задач симплексным методом надо освоить три основных элемента:

· способ определения первоначального допустимого базисного решения

· правило перехода к лучшему решению

· критерий проверки оптимальности найденного решения

Кроме того, для решения задачи симплексным методом, она должна быть представлена в канонической форме (все неравенства должны быть заменены уравнениями). Для этого, если в неравенстве стоит знак ">" или "≥", надо ввести дополнительную переменную в левую часть уравнения, со знаком "-" при её коэффициенте, иначе со знаком "+". И так заменяются все неравенства.

Итак, симплексный метод вносит определенный порядок как при нахождении первого (исходного) базисного решения, так и при переходе к другим базисным решениям. Его идея состоит в следующем.

Имея систему ограничений, приведенную к общему виду, то есть к системе m линейных уравнений с n переменными (m < n), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще.

Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то, осуществляется переход к другому, обязательно допустимому базисному решению.

Симплексный метод гарантирует, что при этом новом решении линейная форма, если и не достигнет оптимума, то приблизится к нему. С новым допустимым базисным решением поступают так же, пока не находят решение, которое является оптимальным.

Если первое найденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляетсяпереход к другим базисным решениям, которые приближают нас к области допустимых решений, пока на каком-то шаге решения либо базисное решение окажется допустимым и к нему применяют алгоритм симплексного метода, либо мы убеждаемся в противоречивости системы ограничений.

Таким образом, применение симплексного метода распадается на два этапа: нахождение допустимого базисного решения системы ограничений или установление факта ее несовместности; нахождение оптимального решения.
При этом каждый этап может включать несколько шагов, соответствующих тому или иному базисному решению. Но так как число базисных решений всегда ограниченно, то ограниченно и число шагов симплексного метода.

12 Следующая ⇒