
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лекция №6
Лекция №6

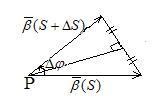
Пусть у нас есть кривая  , где S – натуральный параметр. В точке P построим соприкасающуюся плоскость, нормаль которой совпадает с бинормалью. В точке Q строим соприкасающуюся плоскость, с нормалью
, где S – натуральный параметр. В точке P построим соприкасающуюся плоскость, нормаль которой совпадает с бинормалью. В точке Q строим соприкасающуюся плоскость, с нормалью  . Совершаем параллельный перенос вектора
. Совершаем параллельный перенос вектора  в точку P, угол между
в точку P, угол между 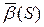 и
и  обозначим
обозначим 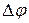 .
.
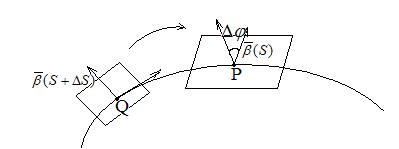
Абсолютным кручением|æ| кривой  в точке P называется
в точке P называется 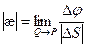 .
.
Теорема. В каждой точке регулярной кривой (хотя бы трижды непрерывно дифференцируемой), где 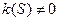 определено значение абсолютного кручения. И если
определено значение абсолютного кручения. И если 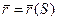 - уравнение данной кривой, то
- уравнение данной кривой, то 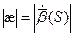
 или
или 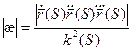 .
.
Доказательство
1) Докажем первую формулу:
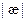
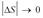
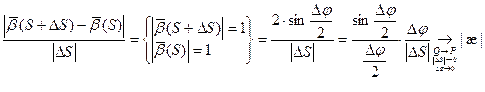
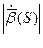 1
1
Получаем: 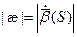 .
.
2) Докажем вторую формулу:
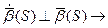
 т.к.
т.к. 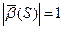 (по лемме).
(по лемме).
Из перпендикулярности 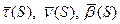 следует, что
следует, что 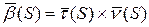 . Продифференцируем это равенство:
. Продифференцируем это равенство: 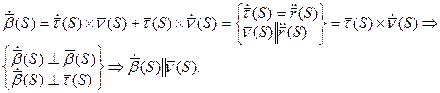
Поэтому  (модуль æ равен модулю скалярного произведения, где
(модуль æ равен модулю скалярного произведения, где 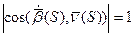 ).
).
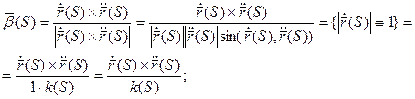
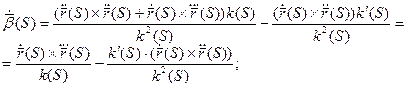
Нормируем вектор 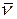 :
:
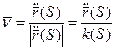 ;
;
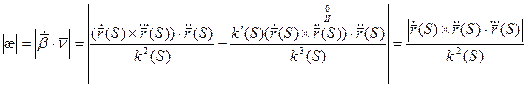 Ч.т.д.
Ч.т.д.
Геометрический смысл модуля кручения:
Степень отклонения кривой от плоскости в каждой точки кривой.
Для винтовой линии кручение является константой.
 |
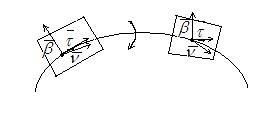
Кручению присваивается знак «+», если при перемещении по кривой в сторону возрастания параметра S поворот соприкасающейся плоскости происходит от 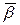 к
к 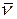 и знак «–», если – от
и знак «–», если – от 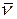 к
к 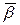 .
.
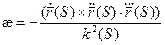 .
.
Утверждение. Если кручение в каждой точке кривой равно нулю, то кривая является плоской.
Доказательство
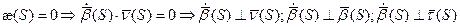
Получаем: 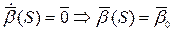 .
.
Уравнение плоской кривой в векторном виде:
 .
.
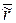 - переменный вектор;
- переменный вектор;
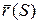 - радиус – вектор точки Р кривой γ;
- радиус – вектор точки Р кривой γ;
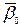 - вектор бинормали. Ч.т.д.
- вектор бинормали. Ч.т.д.
 |
Пусть кривая  задана с помощью произвольной параметризации:
задана с помощью произвольной параметризации:
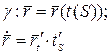
Возводим обе части равенства в квадрат, получим:
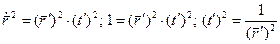 .
.
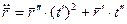 ;
;
 .
.
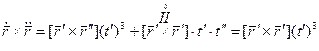 .
.
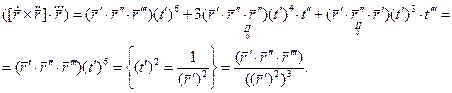
 ;
;
Формула для вычисления кручения при произвольной параметризации:
 .
.
Пример:
Найти кривизну и кручение винтовой линии.
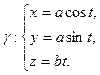

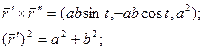
 .
.
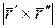 - длина вектора
- длина вектора 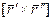 .
.
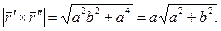
 - не зависит от параметра t, отсюда кривизна винтовой линии величина постоянная.
- не зависит от параметра t, отсюда кривизна винтовой линии величина постоянная.
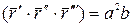 .
.
æ 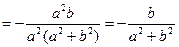 - также не зависит от параметра t.
- также не зависит от параметра t.
 |
В каждой точке хотя бы бирегулярной кривой можно построить трёхгранник Френе.
Выбираем направление единичных векторов 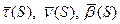 , так чтобы они образовывали правую тройку – базис.
, так чтобы они образовывали правую тройку – базис.
Формулы Френе показывают разложение векторов 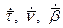 в базисе векторов
в базисе векторов 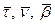 .
.
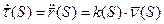 .
.
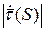 - это есть кривизна.
- это есть кривизна.
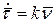 - первая формула Френе.
- первая формула Френе.
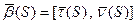 .
.
Продифференцируем, получим:
 .
.
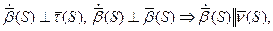
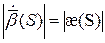 .
.
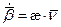 - третья формула Френе.
- третья формула Френе.
 .
.
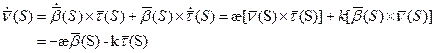
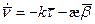 - вторая формула Френе.
- вторая формула Френе.

 |
Если рассматривать трёхгранник Френе в виде твердого тела, которое совершает вращение вокруг точки, то вектор мгновенной угловой скорости
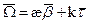 . Этот вектор лежит в спрямляющей плоскости, где æ, k – это проекции данного вектора на вектора
. Этот вектор лежит в спрямляющей плоскости, где æ, k – это проекции данного вектора на вектора 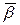 и
и  соответственно.
соответственно.
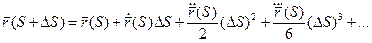
Выберем систему координат, совместив начало системы координат с точкой Р, а оси координат направим по ребрам трёхгранника Френе и выпишем систему, определяющую данную кривую в окрестности данной точки Р.
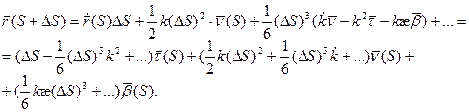
Тогда мы можем записать в параметрическом виде:
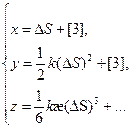 - параметрическое задание кривой, параметр
- параметрическое задание кривой, параметр 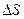 .
.
Спроектируем полученную кривую на плоскости трехгранника Френе:
1) Соприкасающаяся плоскость
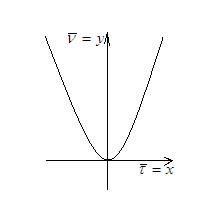 Парабола.
Парабола.
2) Нормальная плоскость
 Полукубическая парабола.
Полукубическая парабола.
3) Спрямляющая плоскость
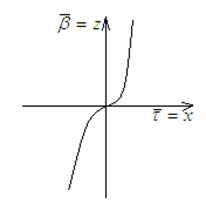 Кубическая парабола.
Кубическая парабола.
При 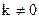 и
и 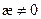 .
.
Коэффициенты разложения функции  в ряд по степеням
в ряд по степеням 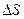 выражаются только через кривизну и кручения кривой. Это дает основание полагать, что кривизна и кручения в какой-то мере определяют кривую.
выражаются только через кривизну и кручения кривой. Это дает основание полагать, что кривизна и кручения в какой-то мере определяют кривую.

Теорема. Пусть 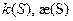 - две некоторые регулярные функции, причем
- две некоторые регулярные функции, причем 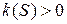 , тогда существует кривая в пространстве, единственная с точностью до расположения в пространстве, для которой
, тогда существует кривая в пространстве, единственная с точностью до расположения в пространстве, для которой 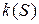 и
и 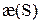 являются кривизной и кручением соответственно в точке, соответствующей значению параметра S.
являются кривизной и кручением соответственно в точке, соответствующей значению параметра S.
Доказательство
Пусть такая кривая существует, тогда 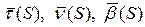 - единичные векторы касательной нормали и бинормали, должны удовлетворять системе дифференциальных уравнений:
- единичные векторы касательной нормали и бинормали, должны удовлетворять системе дифференциальных уравнений:
 (1)
(1)
В силу формул Френе.
Разыскивая кривую с 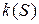 и
и 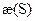 , естественно обратиться к системе дифференциальных уравнений (1).
, естественно обратиться к системе дифференциальных уравнений (1).
Пусть решение системы (1) существует и удовлетворяет начальным условиям:
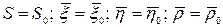 .
.
Причем 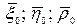 - три взамноперпендикулярных единичных вектора:
- три взамноперпендикулярных единичных вектора: 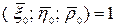 - это правая тройка векторов.
- это правая тройка векторов.
Нужно доказать, что 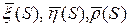 обладают теми же свойствами для любых S, т.е. они единичные, взаимноперпендикулярные и образуют правую тройку векторов.
обладают теми же свойствами для любых S, т.е. они единичные, взаимноперпендикулярные и образуют правую тройку векторов.
Для этого продифференцируем 6 скалярных функций:
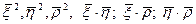 .
.
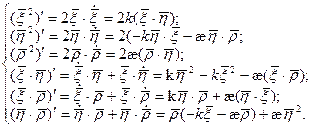
Этой системе удовлетворяет набор констант: 1, 1, 1, 0, 0, 0. И набор функций: 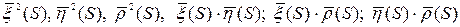 . Оба эти решения совпадают при S=S0, по теореме о единственности решения, функции, выписанные таким образом, совпадают с константами для любых S. Эти функции единичные и взаимноперпендикулярные, поэтому
. Оба эти решения совпадают при S=S0, по теореме о единственности решения, функции, выписанные таким образом, совпадают с константами для любых S. Эти функции единичные и взаимноперпендикулярные, поэтому 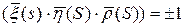 , по непрерывности смешанного произведения, значение этой функции всегда равно +1.
, по непрерывности смешанного произведения, значение этой функции всегда равно +1.
Следовательно, кривую  , можем искать в виде:
, можем искать в виде:
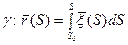 ;
;
Проверим, что S – натуральный параметр:
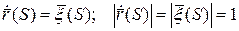 .
.
Подсчитаем кривизну и кручение.
Если параметр натуральный, то кривизну кривой можно найти по формуле: 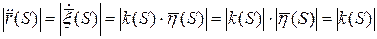 .
.
Если параметр естественный, то кручение считаем по формуле:  .
.
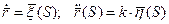 ;
;
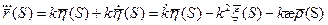 ;
;

Таким образом, кривая  имеет в соответственной точке кривизну
имеет в соответственной точке кривизну 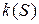 и кручение
и кручение 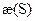 .
.
Существование кривой доказано.
Докажем единственность.
Пусть существуют две кривые 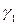 и
и  имеющие в соответственной точке кривизну
имеющие в соответственной точке кривизну 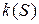 и кручение
и кручение 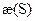 . Совместим эти кривые точками, соответствующими дуге S0, естественными трёхгранниками в этих точках.
. Совместим эти кривые точками, соответствующими дуге S0, естественными трёхгранниками в этих точках.
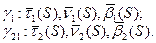
Эти два набора являются решениями системы (1), в точке S=S0 эти векторы совпадают, поэтому они совпадают для любых S.
Получаем:  .
.
Проинтегрировав это равенство, получим: 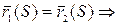 кривые совпадают с точностью до положения в пространстве.
кривые совпадают с точностью до положения в пространстве.
 |
Ч.т.д.
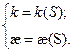
 |
Система таких уравнений называется натуральным уравнением кривой.
1. k=0 – прямые.
2. 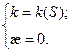 - плоские кривые.
- плоские кривые.
Плоские кривые, у которых 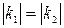 , но разные знаки, будут зеркально симметричными.
, но разные знаки, будут зеркально симметричными.
Движением на плоскости эти кривые совместить нельзя, а в пространстве можно.
Этот случай рассматривают как частный случай пространственных кривых.
3. 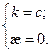 - окружность.
- окружность. 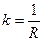 .
.
4. 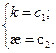 - винтовые линии.
- винтовые линии.
5.  - линии откоса.
- линии откоса.
6. 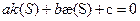 - линии Бертрана.
- линии Бертрана.
Примеры:
I. Найти натуральные уравнения.
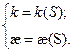
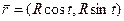 .
.
1). Перейти к натуральной параметризации:
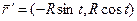 ;
;
 .
.
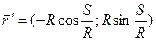 .
.
2). Находим кривизну для естественной параметризации:
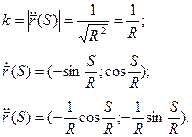
3). Кривая плоская, поэтому  .
.
Получаем: 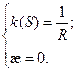
II. Покажем, что она является винтовой линией:
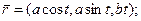
1). Перейдем к натуральной параметризации:
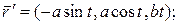

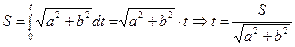 ;
;
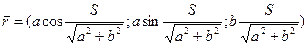 .
.
2). Находим кривизну:
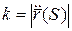
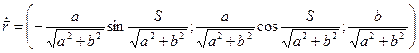 ;
;
 ;
;
 ;
;
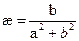 ;
;
Получаем: 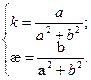 - винтовая линия.
- винтовая линия.
По основной теореме теории кривых, эта система определяет только винтовую линию.
 |
Кривая
 называется линией откоса, если вектор ее касательной образует постоянный угол с некоторым определенным направлением.
называется линией откоса, если вектор ее касательной образует постоянный угол с некоторым определенным направлением.
Представим, что постоянное направление совпадает с вертикалью. Если 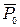 - вертикаль (по определению линии откоса) и
- вертикаль (по определению линии откоса) и 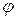 - постоянный угол, то кривизна подъема по кривой
- постоянный угол, то кривизна подъема по кривой  остается постоянной.
остается постоянной.

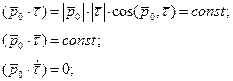
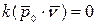 - в силу первой формулы Френе.
- в силу первой формулы Френе.
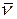 параллельна горизонтальной плоскости.
параллельна горизонтальной плоскости.
В спрямляющей плоскости лежат вектора 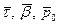 .
.
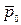 образует с
образует с  постоянный угол по определению линии откоса,
постоянный угол по определению линии откоса,
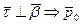 образует с
образует с 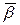 постоянный угол
постоянный угол 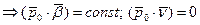 .
.
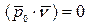 ; где
; где 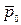 - постоянный вектор.
- постоянный вектор.
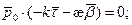
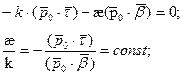
Показали, что 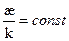 - необходимое условие.
- необходимое условие.
Покажем, что оно же и достаточное условие:
Пусть вдоль кривой 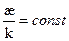 .
.
Запишем вектор  .
.
Из представления вектора 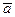 видно, что этот вектор однозначно связан с векторами
видно, что этот вектор однозначно связан с векторами  и
и 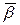 , по длине это постоянный вектор. Остается показать, что
, по длине это постоянный вектор. Остается показать, что 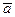 - постоянный вектор и при другом задании кривой он не изменится. Для этого продифференцируем:
- постоянный вектор и при другом задании кривой он не изменится. Для этого продифференцируем:
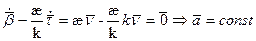 , он удовлетворяет определению данной кривой и образует постоянный угол с
, он удовлетворяет определению данной кривой и образует постоянный угол с  .
.
Получаем: 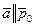 , т.е. показано, что если для некоторой кривой выполнено условие
, т.е. показано, что если для некоторой кривой выполнено условие 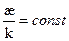 , то данная кривая является линией откоса.
, то данная кривая является линией откоса.
 |
Кривая линия
 называется линией Бертрана, если существует
называется линией Бертрана, если существует 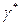 , отличная от
, отличная от  и имеющая с кривой
и имеющая с кривой  общие главные нормали.
общие главные нормали.
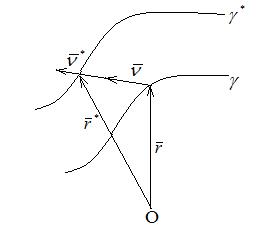
Пусть  , тогда
, тогда  , где а – это фактически длина отрезка заключенная между точками соответствующих кривых.
, где а – это фактически длина отрезка заключенная между точками соответствующих кривых.
Продифференцируем это равенство:
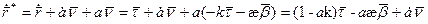 .
.
Домножим обе части скалярно на вектор 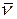 . Получим:
. Получим:
0=0+0+1 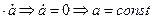 .
.
Главное свойство:
Расстояние между соответствующими точками кривых Бертрана есть постоянная величина.
Вектора 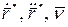 лежат в соприкасающейся плоскости.
лежат в соприкасающейся плоскости.
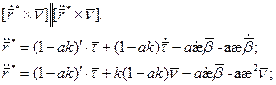

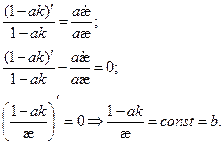
Получим:
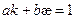 - линейная комбинация скалярных функций k и
- линейная комбинация скалярных функций k и  равна единице. Это уравнение является необходимым условием для линий Бертрана. Покажем, что оно является и достаточным условием.
равна единице. Это уравнение является необходимым условием для линий Бертрана. Покажем, что оно является и достаточным условием.
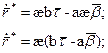
 , где
, где 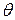 - угол между соответствующими векторами касательных к кривым
- угол между соответствующими векторами касательных к кривым  и
и 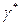 , но
, но 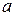 и
и 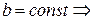
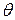 - величина постоянная.
- величина постоянная.
Здесь определяется соответствие между трехгранниками Френе во всех точках кривых Бертрана.
Если 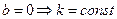 .
.
Рассмотрим случай 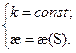 - это косые окружности и их рассматривают как частный случай кривых Бертрана.
- это косые окружности и их рассматривают как частный случай кривых Бертрана.
Пример 1:
Найти уравнение плоской кривой, имеющей натуральные уравнения.
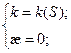
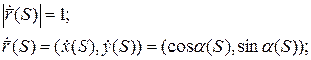
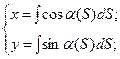 где
где 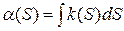 .
.
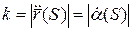 .
.
Пример 2:
Кривая задана 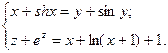 Точка (0;0;0).
Точка (0;0;0).
Найти кривизну кривой в точке.
Параметризуем: пусть х – параметр, а 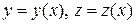 .
.
 ;
;
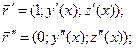
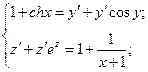
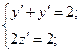
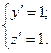
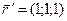 .
.

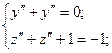
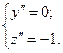
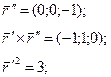
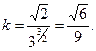
 Лекция №7
Лекция №7
Лемма. Пусть  - аналитическая кривая. О – точка кривой
- аналитическая кривая. О – точка кривой  . При соответствующем выборе системы координат в окрестности точки О кривую
. При соответствующем выборе системы координат в окрестности точки О кривую  можно параметризовать таким образом, что ее уравнение будет иметь вид:
можно параметризовать таким образом, что ее уравнение будет иметь вид:
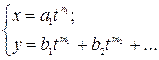
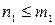 (1)
(1)
Теорема. Пусть аналитическая кривая  задана уравнениями вида (1). Для того, чтобы точка О была особой, необходимо и достаточно, чтобы хотя бы одно из
задана уравнениями вида (1). Для того, чтобы точка О была особой, необходимо и достаточно, чтобы хотя бы одно из 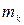 не делилось на
не делилось на 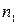 .
.
Теорема. Пусть кривая  задана уравнениями в окрестности т.О:
задана уравнениями в окрестности т.О:
 точка О будет особой точкой, если порядок первых отличных от нуля производных функций x(t) и y(t) в точке О такие, что,
точка О будет особой точкой, если порядок первых отличных от нуля производных функций x(t) и y(t) в точке О такие, что, 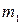 не делиться на
не делиться на 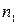 (
( 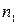 <
< 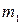 ), причем, если
), причем, если 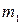 и
и 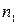 - четные, то точка О – точка возврата II -го рода, а если
- четные, то точка О – точка возврата II -го рода, а если 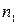 - четное, а
- четное, а 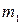 - нечетное, то точка О – точка возврата I-го рода.
- нечетное, то точка О – точка возврата I-го рода.
Если 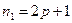 - нечетное, а
- нечетное, а 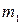 - четное, то в окрестности этой точки кривая ведет себя как обычная кривая.
- четное, то в окрестности этой точки кривая ведет себя как обычная кривая.
Если 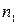 и
и 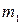 - нечетные, то точка является точкой перегиба.
- нечетные, то точка является точкой перегиба.
Пример:
Определить вид особых точек:
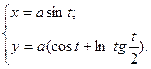
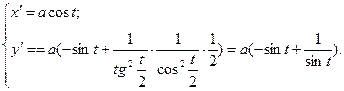
 ;
;
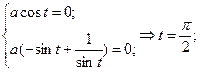
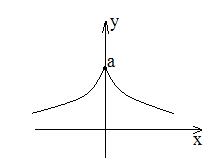 Трактриса.
Трактриса.
 .
.
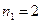 .
.
 ;
;
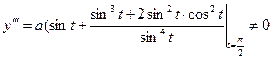 .
.
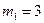 .
.
Точка 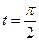 - точка возврата I-го рода.
- точка возврата I-го рода.
Кривая задана неявно.
 .
.
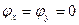 (так определяются особые точки)
(так определяются особые точки)
 , где
, где 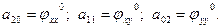
Выпишем уравнение:
(*) 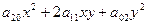 =0 (оно определяет особые точки II-го порядка)
=0 (оно определяет особые точки II-го порядка)
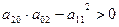 ; (1)
; (1)
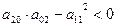 ; (2)
; (2)
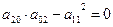 ; (3)
; (3)
При условии (1) уравнение (*) действительных корней не имеет. Данная точка будет изолированной особой точкой.
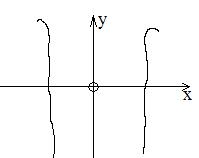
При условии (2) – дает два различных действительных корня:
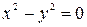 .
.
Случай (2) также дает узловую точку или точку самопересечения.
Условие (3) дает два действительных одинаковых корня:
А) 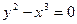
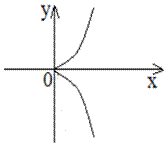 - точка возврата I-го рода.
- точка возврата I-го рода.
Б) 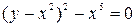
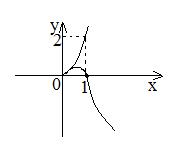 - точка возврата II-го рода.
- точка возврата II-го рода.
В) 
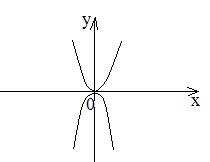 - точка самоприкосновения.
- точка самоприкосновения.
Пример:
1. Исследовать особые точки кривой:
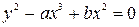 ;
;
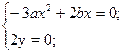

 нашей кривой;
нашей кривой;
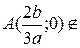 нашей кривой;
нашей кривой;
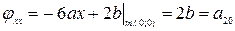 ;
;
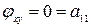 ;
;
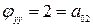 ;
;
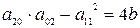 ;
;
1) Если b>0, то точка особая изолированная.
2) Если b<0, то точка узловая.
3) Если b=0, то это либо точка возврата I-го или II-го рода, либо точка самовозврата.
2. Исследовать особые точки кривой:
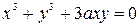 ;
;
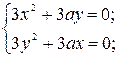
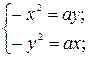
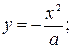
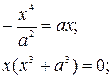
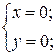
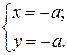
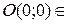 нашей кривой;
нашей кривой;
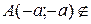 нашей кривой;
нашей кривой;
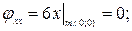
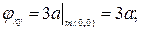
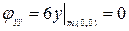 ;
;
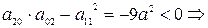 узловая
узловая
Если в особых точках все вторые производные функции  равны нулю, то рассматриваются третьи производные и такие точки называются особыми точками третьего порядка.
равны нулю, то рассматриваются третьи производные и такие точки называются особыми точками третьего порядка.
 |
Пусть
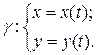
 .
.
Говорят, что кривая  уходит на бесконечность при
уходит на бесконечность при 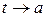 , если выполняется условие
, если выполняется условие 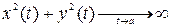 .
.
В этом случае рассматривается вопрос о существовании асимптот.
Прямая g называется асимптотойкривой  , уходящей на бесконечность при
, уходящей на бесконечность при 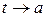 , если выполнено условие
, если выполнено условие 
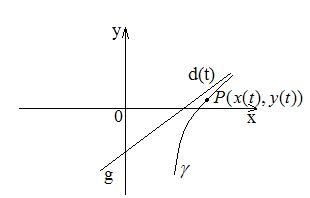
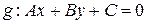 ;
;
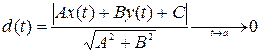 .
.
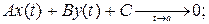
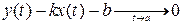 ; - уравнение g.
; - уравнение g.
I. Пусть  .
.
Учитываем условие, что ищем наклонные асимптоты:
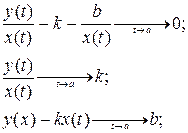
Тогда асимптота имеет вид:
y=kx+b.
Вертикальные асимптоты, параллельны оси Oy, имеют вид:
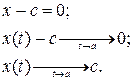
II. Пусть 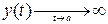 . Проделывая все аналогии, получаем:
. Проделывая все аналогии, получаем:
y=kx+b.
Пример:
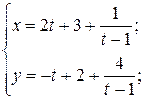
1). Находим точки, в которых кривая уходит на бесконечность:
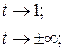
2).  ;
;
 ;
;
Тогда уравнение асимптоты к кривой имеет вид:
у=4х-19;
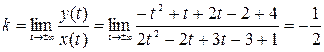 ;
;
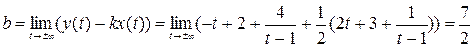 ;
;
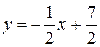 ;
;
Ответ: у=4х-19;
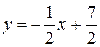 .
.
Пусть кривая γ задана неявно: 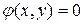 . Касательную ищем в виде:
. Касательную ищем в виде:
(*)  где u – параметр, γ – алгебраическая кривая.
где u – параметр, γ – алгебраическая кривая.
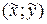 - точка прямой g.
- точка прямой g.
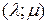 - координаты направляющего вектора прямой.
- координаты направляющего вектора прямой.
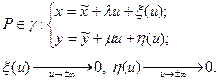
Уравнение нашей кривой: 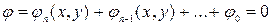 .
.
Подставим (х,у) из (*) в предыдущее уравнение, получим:
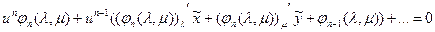 .
.
1) из условия  находим
находим 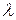 и
и  .
.
2) условие 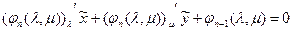 дает уравнение самой асимптоты.
дает уравнение самой асимптоты.
Пример:
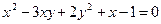 ;
;
1. Вместо х подставляем 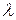 , а вместо у -
, а вместо у -  .
.

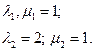
2. 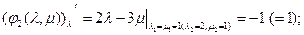
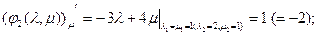

Для первой точки: 
Для второй точки: 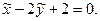
Пример:
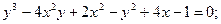
1. 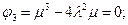
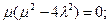
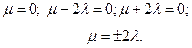


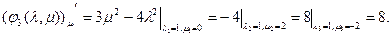
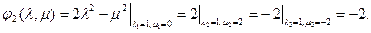
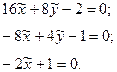
Асимптоту еще называют предельным положением касательной.
 |
Пусть элементарные кривые
 и
и 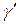 имеют общую точку Р. Возьмем на
имеют общую точку Р. Возьмем на 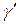 точку Q сколь угодно близкую к Р.
точку Q сколь угодно близкую к Р. 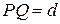 ; h – расстояние от точки Q до кривой
; h – расстояние от точки Q до кривой  .
.

Кривая 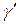 имеет соприкосновение n-го порядка с кривой
имеет соприкосновение n-го порядка с кривой  в точке Р, если
в точке Р, если 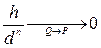 .
.
Теорема. Пусть кривая  :
: 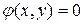 , а кривая
, а кривая 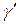 :
:  причем
причем  и
и 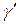 - регулярные кривые. Для того, чтобы кривые
- регулярные кривые. Для того, чтобы кривые  и
и 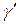 имели соприкосновение n-го порядка в точке Р необходимо и достаточно, чтобы выполнялись условия:
имели соприкосновение n-го порядка в точке Р необходимо и достаточно, чтобы выполнялись условия:

Без доказательства.
Пример:
Найти параболу вида:
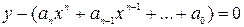 (*)
(*)
имеющую с кривой 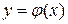 соприкосновение n-го порядка, в т. х=0.
соприкосновение n-го порядка, в т. х=0.
1. Параметризуем кривую:
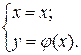 х – параметр.
х – параметр.
2. Подставляем данную точку 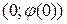 в уравнение (*):
в уравнение (*):
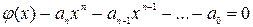 (**)
(**)
 .
.
3. Дифференцируем (**) по х:

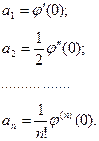
Ответ: искомая парабола  .
.
Окружность, имеющая с кривой соприкосновение второго порядка, называется соприкасающейся окружностьюданной кривой. А центр такой окружности называется центром кривизныданной кривой.
Пример:
Найти уравнение соприкасающейся окружности для  в начале координат.
в начале координат.
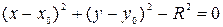 ;
;
Параметризуем данную кривую:
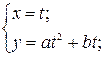
Тогда наша функция примет вид:
 ; (*)
; (*)
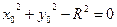 ;
;
Продифференцируем уравнение (*) по t:
 (**)
(**)
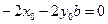 ;
;
Продифференцируем уравнение (**) по t:
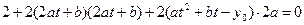 ;
;

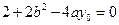 ;
;
 .
.
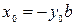 =
= 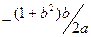 .
.
 .
.

Пусть 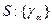 - множество регулярных кривых зависящих от
- множество регулярных кривых зависящих от 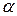 .
.

Гладкая кривая  называется огибающейоднопараметрического семейства
называется огибающейоднопараметрического семейства 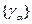 , если в каждой точке она касается хотя бы одной кривой
, если в каждой точке она касается хотя бы одной кривой 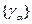 и каждым своим куском
и каждым своим куском  касается бесконечного числа кривых множества
касается бесконечного числа кривых множества 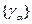 .
.
Всякая регулярная кривая является огибающей семейства своих касательных.
Теорема. Пусть 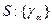 задана уравнением
задана уравнением 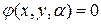 , причем мы предполагаем, что
, причем мы предполагаем, что 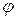 - непрерывно дифференцируемая функция по каждой переменной и выполнено условие
- непрерывно дифференцируемая функция по каждой переменной и выполнено условие  , тогда огибающую данного семейства (если она существует) можно записать в виде:
, тогда огибающую данного семейства (если она существует) можно записать в виде:
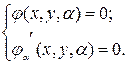
В том смысле, что в каждой точке с координатами (х,у) огибающей  ставится в соответствие значение параметра
ставится в соответствие значение параметра 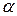 : набор
: набор 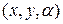 удовлетворяет первому и второму уравнению данной системы.
удовлетворяет первому и второму уравнению данной системы.
Пример:
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|