
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лекция №5
Лекция №1: Понятие кривой. Способы задания кривых...…2
Лекция №2: Вектор-функция скалярного аргумента….……6
Лекция №3: Регулярность кривой. Касательная к кривой...10
Лекция №4: Соприкасающаяся плоскость. Длина дуги
кривой. Естественная параметризация...….....17
Лекция №5: Сопровождающий трехгранник Френе.
Кривизна кривой……………………………....25
Лекция №6: Кручение кривой. Формулы Френе..………...31
Лекция №7: Плоские кривые………………….……………50

1. Погорелов А.В. Дифференциальная геометрия / А.В. Погорелов. – М.: Наука, 1974. – 366 с.
2. Новиков С.П. Элементы дифференциальной геометрии и топологии / С.П. Новиков, А.Т. Фоменко. – М.: Наука, 1987. – 268 с.
3. Аминов Ю.А. Дифференциальная геометрия и топология кривых / Ю.А. Аминов. – М.: Наука, 1987. – 288 с.
4. Постников М.М. Линейная алгебра и дифференциальная геометрия / М.М. Постников. – М.: Наука, 1979. – 196 с.
5. Рашевский П.К. Курс дифференциальной геометрии / П.К. Рашевский. – 5-е изд., испр..- М.: Издательство ЛКИ, 2008. - 432 с.
6. Борисенко О. А. Диференціальна геометрія і топологія: навч. посібник / О. А. Борисенко. - Харьків : Основа, 1995. - 304 с.
 Лекция №1
Лекция №1
Понятие кривой является одним из основных в дифференциальной геометрии. Первоначально этому понятию не давалось точного математического определения.
 Евклид в своих «Началах» называет кривую длиной без ширины или границей поверхности.
Евклид в своих «Началах» называет кривую длиной без ширины или границей поверхности.
 Декарт определяет кривую, как геометрическое место точек на плоскости, координаты каждой из которых удовлетворяет уравнению вида F(x,y)=0.
Декарт определяет кривую, как геометрическое место точек на плоскости, координаты каждой из которых удовлетворяет уравнению вида F(x,y)=0.
 Жордан дал определение кривой: множество точек пространства, координаты которых являются непрерывными функциями
Жордан дал определение кривой: множество точек пространства, координаты которых являются непрерывными функциями 
 Пеано в 1890 году построил такую кривуюс помощью непрерывного отображения отрезка
Пеано в 1890 году построил такую кривуюс помощью непрерывного отображения отрезка  , которая является целым квадратом на плоскости.
, которая является целым квадратом на плоскости.
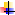 В физике под кривой понимают траекторию движения материальной точки.
В физике под кривой понимают траекторию движения материальной точки.
Элементарная кривая– это топологический образ открытого отрезка. Отображение f называется топологическим (гомеоморфным), если оно взаимнооднозначно, непрерывно и обратное ему отображение также непрерывно.
Примеры элементарных кривых: прямая, графики элементарных функций.
Кривая  называется простой, если множество её точек – связное множество, и каждая точка этой кривой имеет окрестность такую, что та часть окрестности, которая принадлежит
называется простой, если множество её точек – связное множество, и каждая точка этой кривой имеет окрестность такую, что та часть окрестности, которая принадлежит  , представляет собой элементарную кривую (окружность, эллипс и т.д.).
, представляет собой элементарную кривую (окружность, эллипс и т.д.).
Топологический образ простой кривой в пространстве называется общей кривой. Кривая, все точки которой принадлежат некоторой плоскости, называется плоской кривой.

1.
 |
Параметрический:

2. Векторный:

3. Неявный:

Частный случай – явный: y=y(x).
Примеры:
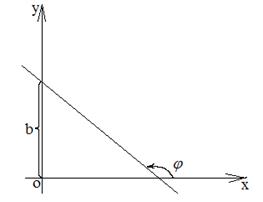
1. y=kx+b;
k=tg  .
.
2.  ;
;
3. 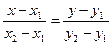 ;
;
4. Ах+Ву+С=0 – общее уравнение прямой,
 - нормаль прямой;
- нормаль прямой;
5. 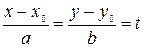 - каноническое уравнение прямой;
- каноническое уравнение прямой;
 - направляющий вектор прямой;
- направляющий вектор прямой;
6.  - параметрическое уравнение прямой;
- параметрическое уравнение прямой;
7.  - окружность;
- окружность;
параметризуем: 
8.  - эллипс (это центрально симметрическая кривая);
- эллипс (это центрально симметрическая кривая);
9.  - гипербола (это центрально симметрическая кривая);
- гипербола (это центрально симметрическая кривая);
10.  - парабола (это не центральная кривая).
- парабола (это не центральная кривая).
Пример:
Написать уравнение движения точки, лежащей на окружности радиуса R, которая катится без проскальзывания с постоянной скоростью v по некоторой прямой.
Решение
Выбираем систему координат.
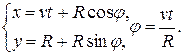


1.  - параметрический способ задания;
- параметрический способ задания;
2.  - векторный способ задания;
- векторный способ задания;
3.  - неявный способ, в виде пересечения двух
- неявный способ, в виде пересечения двух
поверхностей.
Пример:
Написать уравнение траектории движения материальной точки, проекция которой на плоскости хОу движется по окружности  с постоянной угловой скоростью w, а проекция на ось Oz движется поступально с постоянной скоростью b.
с постоянной угловой скоростью w, а проекция на ось Oz движется поступально с постоянной скоростью b.
Решение

Пусть точка M(x,y,z) является точкой заданной кривой

 Лекция №2
Лекция №2
Пусть D некоторое множество, если для  определен вектор
определен вектор  , то говорят, что на области D задана вектор – функция. D=
, то говорят, что на области D задана вектор – функция. D=  .
.

Вектор  , если
, если  .
.
Свойства:
Пусть  , тогда
, тогда
1. 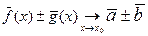 ;
;
2.  ;
;
3. 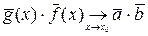 ;
;
4.  .
.
Доказательство 4:
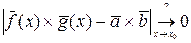

 Ч.т.д.
Ч.т.д.
 непрерывна в точке
непрерывна в точке  , если
, если  .
.
Если 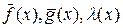 - непрерывны в некоторой точке, то и
- непрерывны в некоторой точке, то и  - непрерывны.
- непрерывны.

 называется дифференцируемой в точке х, если
называется дифференцируемой в точке х, если 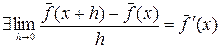 и
и  - производная векторной функции
- производная векторной функции  в точке х.
в точке х.
 .
.
Пусть у нас есть некоторый базис в 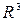 (базис – максимально линейно независимая система векторов данного пространства)
(базис – максимально линейно независимая система векторов данного пространства) 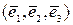 . Пусть дана некоторая вектор – функция
. Пусть дана некоторая вектор – функция 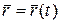 в этом пространстве.
в этом пространстве.

Теорема. Пусть 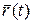 - непрерывна или дифференцируема на некотором множестве D, тогда координатные функции
- непрерывна или дифференцируема на некотором множестве D, тогда координатные функции  являются также непрерывными или дифференцируемы на этом множестве. Верно и обратное утверждение.
являются также непрерывными или дифференцируемы на этом множестве. Верно и обратное утверждение.
Доказательство
Доказательство обратного утверждения очевидно, т.к.  - всегда либо непрерывны, либо дифференцируемы, а сумма непрерывных либо дифференцируемых функций является непрерывной либо дифференцируемой соответственно.
- всегда либо непрерывны, либо дифференцируемы, а сумма непрерывных либо дифференцируемых функций является непрерывной либо дифференцируемой соответственно.
Доказательство прямого утверждения: выберем  ,
,
 .
.
Дифференцируема Дифференцируема
Аналогично доказывается для 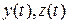 .
.
Ч.т.д.
Пусть 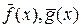 - дифференцируемые вектор – функции, а
- дифференцируемые вектор – функции, а 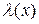 - дифференцируемая скалярная функция, тогда:
- дифференцируемая скалярная функция, тогда:

Примеры:
1. 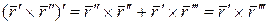 ;
;
2. 
Лемма. Для того, чтобы 
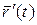 ,
,  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы  .
.
Доказательство
Пусть 
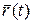
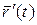
 .
.
 (по условию).
(по условию).
 ;
;
Продифференцируем обе части:
 , следовательно
, следовательно 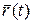
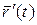 .
.
В обратную сторону. Если 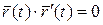 , то
, то  .
.
Ч.т.д.

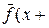 ∆х)=
∆х)=  ∆х+
∆х+ 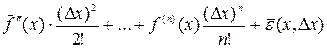 ;
;
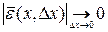 .
.
Выводится с помощью разложения вектор – функции по базису.
Пусть f(x) – непрерывна на  , тогда:
, тогда:
1.  .
.
Пусть  – некоторый постоянный вектор,
– некоторый постоянный вектор,
2.  ;
;
3. 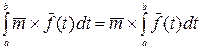 ;
;
4. 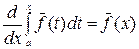 .
.
 Лекция №3
Лекция №3
1. Параметрическое задание кривой:
 эту кривую мы будем называть регулярной, если
эту кривую мы будем называть регулярной, если
выполнены два условия:
1) 
 ,
,
2)  .
.
Если 
 и выполняется второе условие регулярности, то кривая называется гладкой.
и выполняется второе условие регулярности, то кривая называется гладкой.
2. Векторный способ задания:
 эта кривая называется регулярной, если выполнены следующие два условия:
эта кривая называется регулярной, если выполнены следующие два условия:
1) 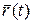
 ,
,
2) 
3. Кривая задана в виде пересечения двух поверхностей:
 кривая регулярная, если:
кривая регулярная, если:
1) 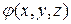 ,
,  - регулярные функции переменных x, y, z,
- регулярные функции переменных x, y, z,
2)  .
.
Точки, где нарушено хотя бы одно условие регулярности, называются особые точки кривой.

1. Кривая задана параметрически:
 кривая называется регулярной, если
кривая называется регулярной, если
1) 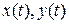
 .
.
2)  .
.
2. Неявное задание кривой:
 кривая называется регулярной, если
кривая называется регулярной, если
1)  регулярная функция переменных х и у,
регулярная функция переменных х и у,
2)  .
.
 .
.
3. Для векторного задания определение регулярности аналогично пространственному.
Регулярность кривой зависит от выбора параметризации этой кривой. Очень часто для кривой  удобно вместо параметра t ввести новый параметр
удобно вместо параметра t ввести новый параметр 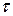 . Другими словами, «пробежаться» по кривой другим способом, точнее в другой шкале времени. Естественно предполагать, что связь между параметрами «гладкая», т.е. функции
. Другими словами, «пробежаться» по кривой другим способом, точнее в другой шкале времени. Естественно предполагать, что связь между параметрами «гладкая», т.е. функции  и
и  непрерывно дифференцируемы до некоторого порядка. Обычно предполагают, что
непрерывно дифференцируемы до некоторого порядка. Обычно предполагают, что  . Это означает, что при такой замене параметра сохраняется направление движения по кривой. Такие замены параметра называют регулярными.
. Это означает, что при такой замене параметра сохраняется направление движения по кривой. Такие замены параметра называют регулярными.
Говорят, что уравнение 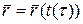 получено заменой параметра на кривой
получено заменой параметра на кривой  . Разумеется, при этом нужно указать область изменения параметра
. Разумеется, при этом нужно указать область изменения параметра 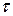 .
.
Регулярная замена параметра не нарушает свойства регулярности кривой, так как
 .
.
Замена параметра на кривой означает изменение криволинейной координаты на кривой. Иногда это приводит к упрощению исследования кривой, в частности её построения.

Касательной к кривой в точке  является предельное положение секущих
является предельное положение секущих  . Векторы
. Векторы 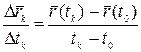 являются направляющими векторами этих секущихся. Поэтому вектор
являются направляющими векторами этих секущихся. Поэтому вектор 
 является направляющим вектором «предельной секущийся», т.е. касательной.
является направляющим вектором «предельной секущийся», т.е. касательной.

Проведем через точку P прямую g.
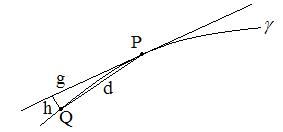
Прямая g называется касательной к кривой  в точке Р, если
в точке Р, если 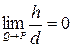 .
.
Теорема. В каждой точке гладкая кривая имеет касательную, причем единственную. И если 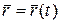 - уравнение кривой, то касательная параллельна вектору
- уравнение кривой, то касательная параллельна вектору 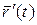 в точке Р, соответствующей параметра t.
в точке Р, соответствующей параметра t.
Доказательство
Пусть g - касательная  ||g. Пусть
||g. Пусть 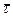 - направляющий вектор прямой g.
- направляющий вектор прямой g.

 .
.

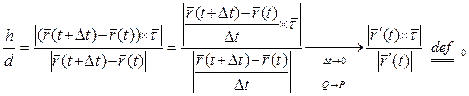 ;
;
 , т.к., по условию теоремы, кривая гладкая
, т.к., по условию теоремы, кривая гладкая  ||
||  .
.
Докажем, что если прямая g||  , то g – касательная.
, то g – касательная.
 .
.
Теорема доказана.
Запишем уравнение касательной:
 .
.
Касательная – это предельное положение секущей.
 .
.
Если  , то
, то  выполняет роль касательного вектора в точке Р кривая
выполняет роль касательного вектора в точке Р кривая  .
.

Векторное задание:

Каноническое задание:
 .
.
Пример:
Написать уравнение касательной для винтовой линии в т.Р.
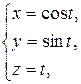 Р(1;0;0)
Р(1;0;0)
Находим значение параметра, соответствующего координатам т.Р, из последнего уравнения получаем t=0. Находим координаты  :
:

 - уравнение касательной к точке Р(1,0,0).
- уравнение касательной к точке Р(1,0,0).

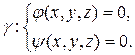
Параметризуем уравнения, считая х, у, z – функции параметра t.
Продифференцируем уравнения системы по t:

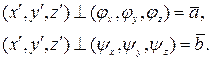
 ||
|| 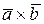 .
.
Уравнение будет иметь вид:
 .
.
Пример:
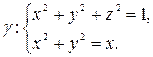 т.Р(0;0;1).
т.Р(0;0;1).

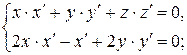
 (0;1;0) – вектор является касательным для
(0;1;0) – вектор является касательным для
искомой прямой в т.Р.
 - уравнение касательной.
- уравнение касательной.

1. Кривая задана параметрически:
 .
.
Уравнение касательной: 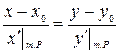 .
.
2. Неявное задание кривой:
 .
.

Уравнение касательной: 
3. Кривая задана явно:
y=y(x).
Уравнение касательной: 
 |
Лекция №4
 |
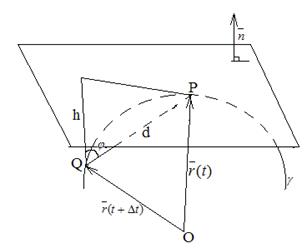
Плоскость 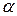 будем называть соприкасающейся с кривой
будем называть соприкасающейся с кривой  в точке Р, если
в точке Р, если 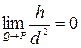 .
.
Теорема. В каждой точке хотя бы дважды регулярной кривой существует соприкасающаяся плоскость. И если 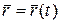 - уравнение кривой
- уравнение кривой  , то
, то 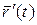 и
и 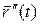 будут параллельны соприкасающейся плоскости в точке Р, соответствующей параметру t.
будут параллельны соприкасающейся плоскости в точке Р, соответствующей параметру t.
Доказательство
Докажем, что 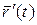 ,
, 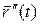 ||
|| 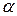 , если плоскость
, если плоскость 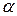 соприкасается с кривой
соприкасается с кривой  в точке Р.
в точке Р.
 .
.
 .
.
Теперь воспользуемся определением соприкасающейся плоскости
 .
.
Разложим 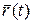 в ряд Тейлора по степеням
в ряд Тейлора по степеням  в окрестности т.Р.
в окрестности т.Р.
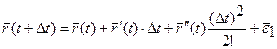 ;
;
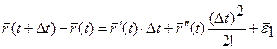 ;
;
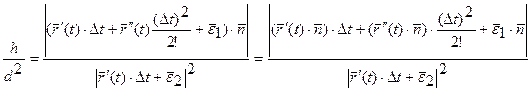

Т.к. по условию теоремы кривая дважды регулярна, то  ,
,  ||
|| 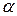 ,
,
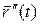 ||
|| 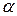 .
.
Т.о., если соприкасающаяся плоскость существует, то 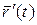 и
и 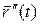 параллельны ей.
параллельны ей.
Докажем существование соприкасающейся плоскости. Пусть плоскость 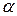 ||
||  и
и 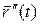 , тогда
, тогда  ,
, 
 .
.
Т.о. в каждой точке регулярной кривой существует соприкасающаяся плоскость.
Если рассматривать кривую, для которой нарушены условия бирегулярности, но она является гладкой кривой, то соприкасающиеся плоскости существуют и их бесконечно много, т.е. это любая плоскость содержащая касательную.
Теорема доказана.

 ||
||  ,
,
 .
.
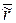 - переменный радиус вектор, описывающий точки данной плоскости.
- переменный радиус вектор, описывающий точки данной плоскости.
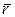 - фиксированное значение вектор – функции в точке Р.
- фиксированное значение вектор – функции в точке Р.

 .
.
 .
.
Пример:
Написать уравнение соприкасающейся плоскости для простой винтовой линии в точке Р(1;0;0).
 Р(1;0;0).
Р(1;0;0).
Определим значение параметра t.
t=0.
Дифференцируем:

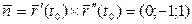
Составить уравнение плоскости через точку Р перпендикулярно вектору 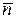 .
.
0(x-1)-1(y-0)+1(z-0)=0,
y-z=0 – уравнение соприкасающейся плоскости.

 Пусть
Пусть  - некоторая элементарная кривая. Впишем в
- некоторая элементарная кривая. Впишем в  ломанную
ломанную  .
.


Пусть  топологический образ некоторого отрезка прямой g.
топологический образ некоторого отрезка прямой g.
Ломанная  называется правильно вписаннойв
называется правильно вписаннойв  , если порядок прообразов её вершин на прямой g совпадает с порядком вершин на
, если порядок прообразов её вершин на прямой g совпадает с порядком вершин на  .
.
Свойство ломанной  быть правильно вписанной в
быть правильно вписанной в  не зависит от гомеоморфизма f.
не зависит от гомеоморфизма f.
Кривая  называется спрямляемойв окрестности точки, если эта точка имеет такую окрестность, что все ломанные, правильно вписанные в неё, равномерно ограничены по длине.
называется спрямляемойв окрестности точки, если эта точка имеет такую окрестность, что все ломанные, правильно вписанные в неё, равномерно ограничены по длине.
Кривая  называется спрямляемой, если она спрямляема в окрестности каждой точки.
называется спрямляемой, если она спрямляема в окрестности каждой точки.
Длиной дуги кривой  называется верхняя грань длин правильно вписанных в неё звеньев ломанных.
называется верхняя грань длин правильно вписанных в неё звеньев ломанных.
Рассмотрим в параметризации вида простой кусок или элементарную кривую.
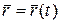 ;
;
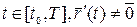 .
.
Для вычисления разобьем промежуток  на части (n – частей).
на части (n – частей).

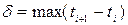 .
.

Периметр ломаной обозначим: 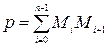 .
.
S – длина простого куска.
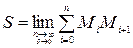 .
.
Будем считать, что 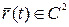 , из рисунка -
, из рисунка -  .
.
Напишем ряд Тейлора:
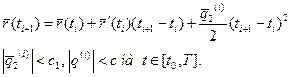
 . (*)
. (*)
 .
.
В точке  проведем
проведем  - вектор касательной.
- вектор касательной.
Введем  .
.

 .
.
Покажем, что 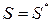 .
.

Применим формулу (*), получим
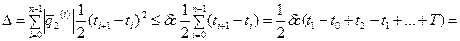
 .
.
 , тогда правая часть
, тогда правая часть  , это означает, что
, это означает, что 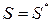 и для длины простого куска имеет место следующая формула:
и для длины простого куска имеет место следующая формула:
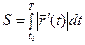 .
.
В скалярном виде: 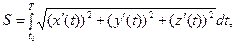 если
если
 |
 .
.
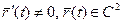 .
.
Регулярная замена переменных  .
.
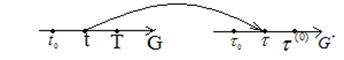
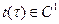 ,
,

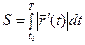 ,
,
 , где
, где 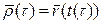 ,
,
 ,
,
 , т.к.
, т.к.  .
.

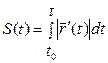 - длина дуги
- длина дуги  кривой
кривой  .
.
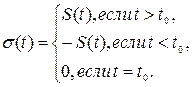
Функция  строго монотонна,
строго монотонна, 
 можно принять за параметр.
можно принять за параметр.
 - естественная параметризация.
- естественная параметризация.
 - нормированный вектор.
- нормированный вектор.
 .
.
Если кривая задана с помощью естественной параметризации, то  .
.
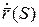 - дифференцируем по естественному параметру.
- дифференцируем по естественному параметру.
Пример:
Для простой винтовой линии перейти от произвольной к естественной параметризации.
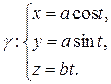
 ;
;


S является натуральным параметром.
Проверка:

Лекция №5
 Из множества нормалей (прямые
Из множества нормалей (прямые  касательным) выберем две: I – лежит в соприкасающейся плоскости – главная нормаль кривой, II – перпендикулярна соприкасающейся плоскости – бинормальная.
касательным) выберем две: I – лежит в соприкасающейся плоскости – главная нормаль кривой, II – перпендикулярна соприкасающейся плоскости – бинормальная.
Если  (хотя бы бирегулярная кривая), то в каждой точке кривой можно построить ортонормированный базис.
(хотя бы бирегулярная кривая), то в каждой точке кривой можно построить ортонормированный базис.
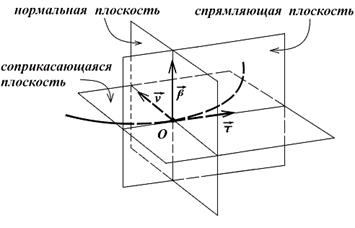
 - единичный вектор касательной;
- единичный вектор касательной;
 - единичный вектор главной нормали;
- единичный вектор главной нормали;
 - единичный вектор бинормали.
- единичный вектор бинормали.
На трех векторах  ,
, 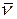 ,
, 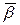 строится трёхгранник, рёбрами которого являются прямые проходящие через точку Р и параллельны векторам
строится трёхгранник, рёбрами которого являются прямые проходящие через точку Р и параллельны векторам  ,
, 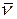 ,
, 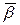 соответственно, а гранями – 3 плоскости:
соответственно, а гранями – 3 плоскости:
 и
и 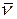 - соприкасающаяся плоскость;
- соприкасающаяся плоскость;
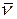 и
и 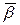 - нормальная плоскость;
- нормальная плоскость;
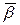 и
и  - спрямляющая плоскость.
- спрямляющая плоскость.
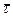 ||
||  ;
;  .
.
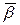 ||
||  .
.
 .
.
 - кривая задана естественной параметризацией.
- кривая задана естественной параметризацией.
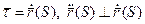 (по лемме, т.к.
(по лемме, т.к.  ).
).
 параллельна соприкасающейся плоскости.
параллельна соприкасающейся плоскости.
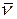 ||
||  .
.
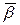 ||
||  .
.
Пример:
Написать уравнение элементов трёхгранника Френе для винтовой линии.
 Р(1;0;0), t=0.
Р(1;0;0), t=0.
1. Проверяем, является ли t естественным параметром.

 , t – произвольный параметр.
, t – произвольный параметр.
2.  ||
|| 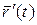 .
.
 ;
;
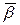 ||
||  (0;-1;1);
(0;-1;1);
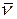 ||[
||[ 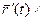
 ]=(2;0;0)||(1;0;0).
]=(2;0;0)||(1;0;0).
3. Напишем уравнение касательной:
 ;
;
4.  - бинормаль;
- бинормаль;
5.  - главная нормаль;
- главная нормаль;
6. Напишем уравнение соприкасающейся плоскости:
0(x-1)-1(y-0)+1(z-1)=0;
y-z=0;
7. Напишем уравнение нормальной плоскости:
0(x-1)+1(y-0)+1(z-1)=0;
y+z=0;
8. Напишем уравнение спрямляющей плоскости:
1(x-1)+0(y-0)+0(z-0)=0; x-1=0.
 |



 .
.
Кривизной кривой в точке Р называется  , где
, где  - длина дуги
- длина дуги  , заключенная между точками P и Ө.
, заключенная между точками P и Ө.
k показывает степень отклонения кривой от прямой.
Физический смысл: модуль скорости изменения вектора  при движении по
при движении по  , т.е. модуль вектора ускорения при естественной параметризации.
, т.е. модуль вектора ускорения при естественной параметризации.
Теорема. В каждой точке регулярной кривой (хотя бы дважды непрерывно дифференцируемой) определена кривизна кривой. И если  - естественная параметризация, то
- естественная параметризация, то 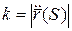 в точке Р, соответствующей параметру S.
в точке Р, соответствующей параметру S.
Доказательство



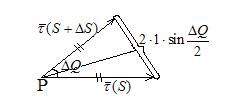
 ,
,
 ;
;
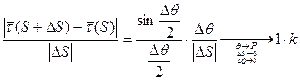
Ч.т.д.

 - кривая задана векторно;
- кривая задана векторно;

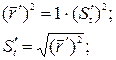

Продифференцируем последнее уравнение, получим:


 ;
;
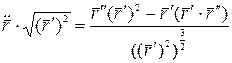 ;
;
Последнее уравнение возведем в квадрат, имеем:
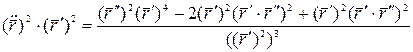
 ;
;
 ;
;
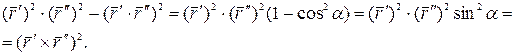
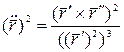 ;
;  .
.
Если кривая плоская, т.е.  то
то  .
.
Если кривая задана явно:y=y(x), то  .
.
Для плоских кривых кривизне присваивают знак.

 |
· Если кривизна в каждой точке кривой равна нулю, то кривая представляет собой либо прямую, либо отрезок прямой. Верно и обратное утверждение.
Доказательство
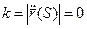 ; В другую сторону:
; В другую сторону:
 ;
;  ;
;
 ;
;  ,
,  ;
;
 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|