
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Некоторые задачи теории массового обслуживания
§ 5. Некоторые задачи теории массового обслуживания
Системы массового обслуживания СМО − системы, предназначенные для многократного использования при решении однотипных задач. Каждая система состоит из определенного количества обслуживающих единиц − каналов.
Будем рассматривать многоканальные СМО с отказами (т.е. такие, в которых в случае занятости всех каналов заявка покидает систему необслуженной). Для них введем следующие показатели.
1. 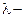 интенсивность потока заявок, т.е. среднее количество заявок, поступающих за единицу времени;
интенсивность потока заявок, т.е. среднее количество заявок, поступающих за единицу времени;
2. 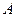 — абсолютная пропускная способность СМО, т.е. среднее число заявок, рассматриваемых в единицу времени.
— абсолютная пропускная способность СМО, т.е. среднее число заявок, рассматриваемых в единицу времени.
3. 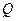 — относительная пропускная способность, т.е. средняя доля пришедших заявок, обслуживаемых системой.
— относительная пропускная способность, т.е. средняя доля пришедших заявок, обслуживаемых системой.
4. 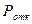 — вероятность отказа, т.е. того, что заявка покинет систему необслуженной.
— вероятность отказа, т.е. того, что заявка покинет систему необслуженной.
5. 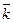 — среднее число занятых каналов для многоканальной системы.
— среднее число занятых каналов для многоканальной системы.
6. 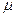 — интенсивность обслуживания, т.е. количество заявок, обслуживаемых одним каналом за единицу времени.
— интенсивность обслуживания, т.е. количество заявок, обслуживаемых одним каналом за единицу времени.
7. 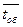 — среднее время обслуживания, т.е.
— среднее время обслуживания, т.е. 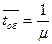 .
.
Итак, имеется 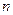 каналов, на которые поступает поток заявок с интенсивностью
каналов, на которые поступает поток заявок с интенсивностью 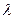 . Поток обслуживания каждого канала имеет интенсивность
. Поток обслуживания каждого канала имеет интенсивность 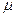 . Найдем предельные вероятности состояний системы и показатели ее эффективности.
. Найдем предельные вероятности состояний системы и показатели ее эффективности.
Система 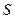 имеет следующие состояния
имеет следующие состояния 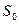 ,
, 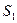 ,
, 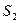 , …,
, …, 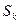 , …,
, …, 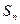 , пронумерованные по числу заявок, находящихся в системе, т.е.
, пронумерованные по числу заявок, находящихся в системе, т.е. 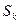 — состояние системы, когда в ней находятся
— состояние системы, когда в ней находятся 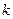 заявок (занято
заявок (занято 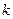 каналов).
каналов).
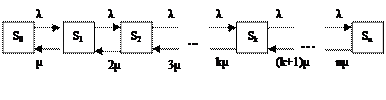 Граф состояний соответствует процессу гибели и размножения.
Граф состояний соответствует процессу гибели и размножения.
Переход в соседнее состояние с большим номером всегда происходит под действием простейшего потока с интенсивностью 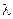 , а вот переход из состояния
, а вот переход из состояния 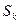 в состояние
в состояние 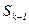 происходит под действием потока интенсивности
происходит под действием потока интенсивности 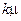 , так как освободиться может любой из
, так как освободиться может любой из 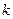 занятых каналов.
занятых каналов.
Формула для предельной вероятности состояния 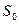 примет вид
примет вид
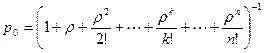 , (1)
, (1)
где 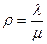 — так называемая интенсивность нагрузки канала, а
— так называемая интенсивность нагрузки канала, а
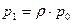 ,
, 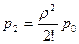 , …,
, …, 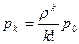 , …,
, …, 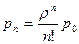 . (2)
. (2)
Найдем показатели эффективности СМО.
Вероятность отказа системы есть предельная вероятность того, что все 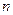 каналов будут заняты, т.е.
каналов будут заняты, т.е.
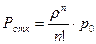 .
.
Относительная пропускная способность — вероятность того, что заявка будет обслужена
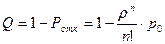 .
.
Абсолютная пропускная способность
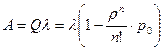 .
.
Среднее число занятых каналов 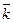 , т.е. математическое ожидание числа занятых каналов
, т.е. математическое ожидание числа занятых каналов
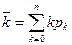 или иначе
или иначе 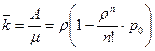 .
.
Далее разбирайте задачи к практическому занятию и используйте методички (см. список литературы).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|