
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Процессы гибели и размножения
Для изучения процессов с дискретными состояниями пользуются так называемым графом состояний, в котором состояния системы обозначаются прямоугольниками или кружочками, а возможные переходы из состояния в состояние − ориентированными дугами графа.
I. Рассмотрим марковский процесс с дискретным состоянием и дискретным временем.
Пусть имеется физическая система 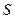 , которая может находиться в состояниях
, которая может находиться в состояниях 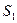 ,
, 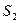 , …,
, …, 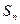 , причем переход системы из состояния в состояние осуществляется скачками только в моменты времени
, причем переход системы из состояния в состояние осуществляется скачками только в моменты времени 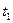 ,
, 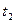 , …,
, …, 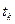 , …, для которых разности
, …, для которых разности 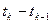 равны постоянному числу — шагу, для простоты принимаемому за единицу времени. Такие марковские процессы называются марковскими цепями.
равны постоянному числу — шагу, для простоты принимаемому за единицу времени. Такие марковские процессы называются марковскими цепями.
Определение. Вероятностью состояния 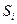
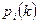 называется вероятность системы
называется вероятность системы 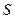 находиться в состоянии
находиться в состоянии 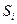 после
после 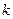 -го шага.
-го шага.
Очевидно, что для каждого шага 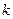
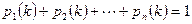 .
.
Будем считать, что вероятности 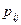 перехода системы из состояния
перехода системы из состояния 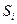 в состояние
в состояние 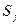 (они называются переходными вероятностями) одинаковые для всех шагов (такая цепь называется однородной).
(они называются переходными вероятностями) одинаковые для всех шагов (такая цепь называется однородной).
Введем так называемую матрицу вероятностей перехода
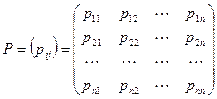 . (1)
. (1)
Элементы матрицы 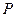 неотрицательны, но могут равняться 0:
неотрицательны, но могут равняться 0: 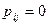 , если переход системы
, если переход системы 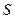 из состояния
из состояния 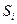 в состояние
в состояние 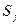 невозможен. Сумма элементов любой строки матрицы
невозможен. Сумма элементов любой строки матрицы 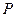 равна 1. Такие матрицы называются стохастическими.
равна 1. Такие матрицы называются стохастическими.
1. Вероятности перехода из состояния 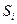 в состояние
в состояние 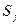 за
за 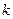 шагов
шагов 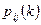 определяются матрицей
определяются матрицей
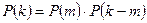 ,
,
где 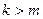 , откуда следует, что
, откуда следует, что
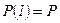 ,
,
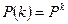 . (2)
. (2)
2. Теорема Маркова. Если при некотором 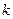 все элементы матрицы
все элементы матрицы 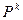 положительны, то существуют такие положительные числа
положительны, то существуют такие положительные числа 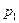 ,
, 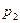 , …,
, …, 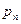 , что независимо от начального состояния системы
, что независимо от начального состояния системы 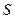 имеют место равенства
имеют место равенства
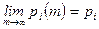 , причем
, причем
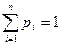 . (3)
. (3)
Вектор 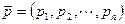 называется предельным распределением, а числа
называется предельным распределением, а числа 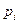 — предельными вероятностями состояний.
— предельными вероятностями состояний.
Предельное распределение 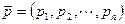 можно найти как собственный вектор матрицы
можно найти как собственный вектор матрицы 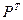 (
( 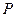 транспонированная), соответствующий собственному значению
транспонированная), соответствующий собственному значению 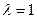 .
.
Пример 2. Задана матрица 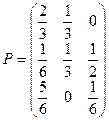 вероятностей перехода цепи Маркова из состояния
вероятностей перехода цепи Маркова из состояния 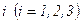 в состояние
в состояние 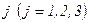 за один шаг. Найти матрицу
за один шаг. Найти матрицу 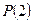 перехода из состояния
перехода из состояния 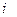 в состояние
в состояние 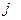 за два шага и вероятность появления цепочки состояний
за два шага и вероятность появления цепочки состояний 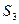 —
— 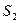 —
— 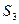 за два шага. Выяснить, можно ли к матрице применить теорему Маркова. Если да, найти предельное распределение.
за два шага. Выяснить, можно ли к матрице применить теорему Маркова. Если да, найти предельное распределение.
Решение. 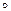 Матрицу
Матрицу 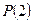 получаем по формуле (2)
получаем по формуле (2)
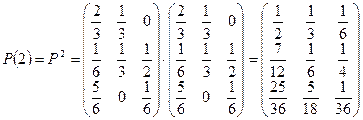 .
.
Вероятность появления цепочки состояний 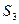 —
— 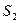 —
— 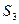 за два шага равна
за два шага равна 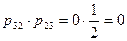 , т.е. такой последовательности состояний наблюдаться не может.
, т.е. такой последовательности состояний наблюдаться не может.
Матрица 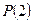 получилась положительной, а это означает, что предельные вероятности существуют. Найдем вектор
получилась положительной, а это означает, что предельные вероятности существуют. Найдем вектор 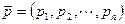 как собственный вектор матрицы
как собственный вектор матрицы
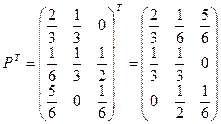
из матричного уравнения
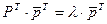 (4)
(4)
при 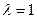 , т.е.
, т.е.
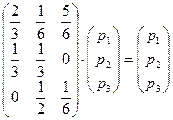 или из системы
или из системы
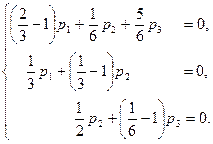
Эта система равносильна системе
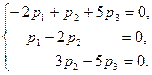
Решая ее, например методом Жордана-Гаусса, получим
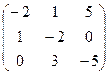 ~
~ 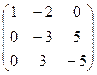 ~
~ 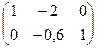 , откуда
, откуда
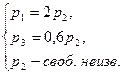
А с учетом (3)
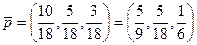 ,
,
т.е. в стационарном режиме система в среднем 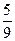 всего времени находится в состоянии
всего времени находится в состоянии 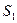 ,
, 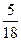 — в состоянии
— в состоянии 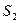 и
и 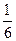 — в состоянии
— в состоянии 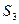 .
. 
II. Рассмотрим марковский процесс с дискретным состоянием и непрерывным временем временем.
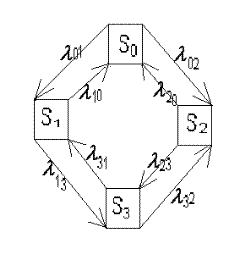
Для таких процессов рисуется граф состояний, вершины которого соответствуют состояниям S0, S1,…,Sn, а дуги − переходам из одного состояния в другое. Как правило, переход из одного состояния в другое происходит под действием простейшего потока событий с интенсивностью 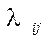 . Граф, дугам которого приписаны интенсивности
. Граф, дугам которого приписаны интенсивности 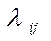 , называется размеченным.
, называется размеченным.
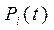 − вероятность того, что в момент времени
− вероятность того, что в момент времени 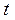 система находиться в состоянии
система находиться в состоянии 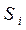 .
.
Для вероятностей 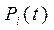 имеет место условие нормировки:
имеет место условие нормировки:
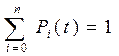 (1)
(1)
и система уравнений Колмогорова:
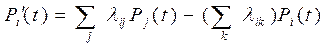 (2)
(2)
Где 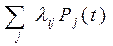 берётся по всем состояниям
берётся по всем состояниям 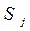 , дуги из которых идут в состояния
, дуги из которых идут в состояния 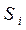 . Во второй сумме берутся все состояния
. Во второй сумме берутся все состояния 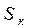 , в которые идут дуги из состояния
, в которые идут дуги из состояния 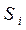 .
.
Особый интерес представляет случай, когда система может перейти в стационарный режим.
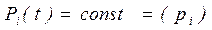 ,
, 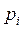 − это предельные вероятности, получающиеся при
− это предельные вероятности, получающиеся при 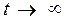 . Их находят из системы:
. Их находят из системы:
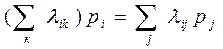
(3)
Среди системы уравнений (3) одно лишнее (любое), его следует отбросить и добавить условие (1). Доказано, что если число состояний конечно и из каждого состояния можно перейти в любое другое, то предельные вероятности существуют.
Пример:
Найти предельные вероятности для системы, размеченный граф которой имеет вид.
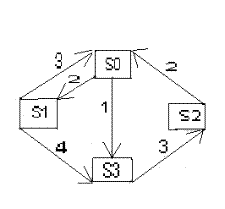

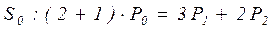 ,
,
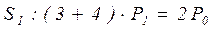 ,
,
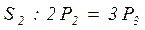 ,
,
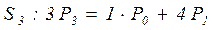 .
.
С учетом условия нормировки получаем систему
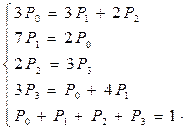
Отбрасываем третье из уравнений, получаем:
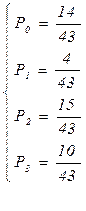
§ 4 Процессы гибели и размножения
описывают изменение численности биологических популяций.
Граф состояний процесса гибели и размножения имеет вид
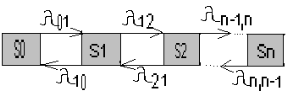
т.к. переход из любого состояния может осуществляться только в состояния с соседними номерами.
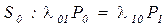 ,
,
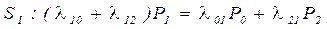 , т.к.
, т.к. 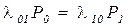 , то остается
, то остается
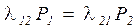 ,
,
и далее аналогично
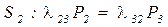 ,
,
…………………..
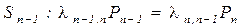 ,
,
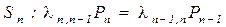 .
.
Получаем систему
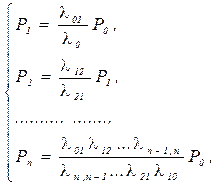
из которой с учетом условия нормировки получаем окончательно
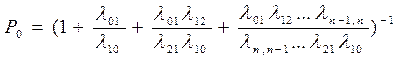 и далее из системы находим
и далее из системы находим 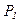 ,
, 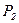 ,…,
,…, 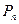 .
.
Пример.Дан граф процесса гибели и размножения.
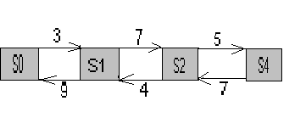
Найдите предельные вероятности состояний.
Решение. 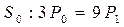 ,
,
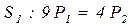 ,
,
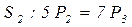 ,
,
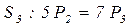 .
.
Отбрасываем последнее уравнение, добавляем условие нормировки и получаем систему
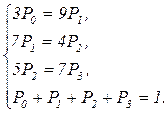 или
или 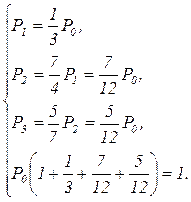
Окончательно
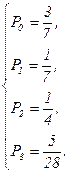
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|