Структурные средние.

3. Структурные средние.

К категории структурных средних относятся мода и медиана. В отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, структурные средние выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решении ряда практических задач.

Мода - значение признака, наиболее часто встречающегося в изучаемой совокупности.

Для дискретного ряда распределения мода определяется визуально: просматривается ряд распределения и то значение признака, которое встречается чаще всего и будет соответствовать моде. Количество мод в одном ряде распределения может быть несколько.

Для интервального ряда распределения сначала определяется модальный интервал. Им будет интервал или интервалы наиболее часто встречающиеся в изучаемой совокупности. Выбрав модальный интервал, моду определяют по формуле:

где X_Mo - нижняя граница модального интервала;

h_Mo - величина модального интервала;

f_Mo - частота модального интервала;

f_Mo-1- частота интервала, предшествующего модальному;

f_Mo+1- частота интервала, следующего за модальным.

Моду можно определить и графически по гистограмме распределения.

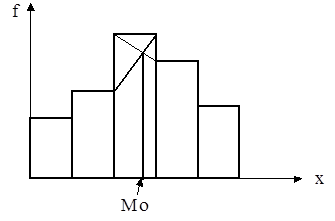
Для этого правую вершину модального прямоугольника соединяют отрезком с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника — с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения.

Медиана - это значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.

Ранжированный ряд - это ряд составленный из значений признаков, расположенных в порядке возрастания или убывания признака.

Для первичных (несгруппированных) данных и дискретного ряда распределения медиана может быть определена по формуле:

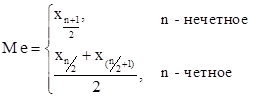Для интервального ряда распределения сначала определяют медианный интервал. Медианным является первый интервал, в котором сумма накопленных частот равна или больше половины общего числа наблюдений: S_Me³ 0.5×n. Выбрав медианный интервал, определяют медиану по одной из формул:

; ,

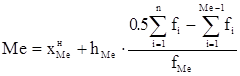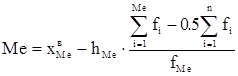где - нижняя граница медианного интервала;

- верхняя граница медианного интервала;

h_Me - величина медианного интервала;

f_Me - частота медианного интервала;

- сумма частот всех интервалов ряда;

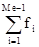- сумма частот интервалов, предшествующих медианному;

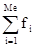- сумма частот медианного интервала и всех ему предшествующих.

Медиана может быть определена и графически по кумулятивной кривой. Для ее определения высоту наибольшей ординаты, которая соответствует общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятивной кривой. Абсцисса точки пересечения является медианой.

Примеры определения медианы:

Пример 1.

Исходные данные:

x: 1.1 2.0 4.1 3.5 6.3 0.4 0.2 7.9 5.6

n=9 - нечетное.

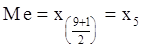Ранжированные данные (по возрастанию):

Me=x₅

x: 0.2 0.4 1.1 2.0 3.5 4.1 5.6 6.3 7.9

i: 1 2 3 4 5 6 7 8 9

Пример 2.

Исходные данные:

x: 1.0 5.0 4.0 7.0 3.0 6.0 0.0 2.0 8.0 9.0

n=10 - четное.

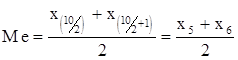Ранжированные данные (по возрастанию):

x₅ x₆

¯ ¯

x: 0.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0

i: 1 2 3 4 5 6 7 8 9

Me=0.5×(4.0+5.0)=4.5.

Пример 3.

Исходные данные:

x’_i	f_i	S_i



			>15, >16



n=Sf=30 - четное

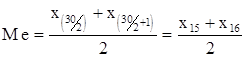Если S_j³ k (j=1,m), то х_k = х’_j, x_k - искомый элемент совокупности с порядковым номером в ранжированном ряду k. В нашем случае х₁₅, х₁₆.

S₄=20 > k=15 Þ x₁₅=x’₄=4.

S₄=20 > k=16 Þ x₁₆=x’₄=4.

Me=0.5×(4+4)=4.

Пример 4.

x	f	S
0-2
2-4
4-6			Медианный интервал: S ³ (n/2)
6-8
8-10

n=Sf=24

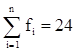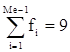, , , f_Me=9, d_Me=2.

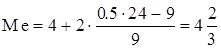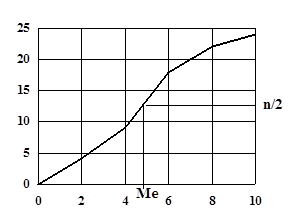
Мода применяется при экспертных оценках, при изучении спроса: при определении наиболее ходовых размеров обуви, одежды и др. товаров, что учитывается при планировании их производства.

Медиана используется при статистическом контроле качества продукции и технологического процесса на промышленных предприятиях; при изучении распределения семей по уровню дохода и др.

Средняя арифметическая, мода и медиана используются для характеристики среднего значения признака в совокупности и относятся к показателям центра распределения.

⇐ Предыдущая 12