Тема 5.Средние величины.. Понятие средней величины.. Степенные средние.

Стр 1 из 2Следующая ⇒

Тема 5.Средние величины.

План:

1. Понятие средней величины.

2. Степенные средние.

3. Структурные средние.

1. Понятие средней величины.

Средней величиной называют значение признака, наиболее характерного для изучаемой совокупности.

Объективность и типичность статистической средней обеспечивается лишь при определенных условиях.

Первое условие — средняя должна вычисляться для качественно однородной совокупности. Для получения однородной совокупности необходима группировка данных, поэтому расчет средней должен сочетаться с методом группировок.

Второе условие — для вычисления средних должны быть использованы массовые данные. В средней величине, вычисленной на основе данных о большом числе единиц совокупности, колебания величины признака, вызванные случайными причинами, погашаются и проявляется общее свойство (типичный размер) признака для всей совокупности.

Средняя величина всегда имеет ту же размерность, что и признак у отдельных единиц совокупности.

В экономических исследованиях и плановых расчетах применяются две категории средних:

- степенные средние;

- структурные средние.

К категории степенных средних относятся:

- средняя арифметическая;

- средняя гармоническая;

- средняя квадратическая;

- средняя геометрическая.

2. Степенные средние.

Формулы средних величин могут быть получены на основе степенной средней, для которой определяющей функцией является уравнение:

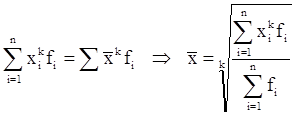где f - веса средней (статистические веса), в качестве которых могут выступать : частота признака, частость и другие величины.

Формулы различных видов степенных средних

Значе	Наименование	Формула средней
ние k	средней	простая	взвешенная
-1	Гармоническая
	Геометрическая
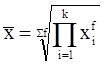
	Арифметическая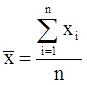
	Квадратическая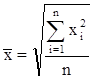

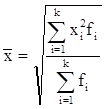
Средняя арифметическая и средняя гармоническая наиболее распространенные виды средней, получившие широкое применение в плановых расчетах, при расчете общей средней из средних групповых, а также при выявлении взаимосвязи между признаками с помощью группировок. Выбор средней арифметической и средней гармонической определяется характером имеющейся в распоряжении исследователя информации.

Пример:

Необходимо вычислить среднюю заработную плату в целом по трем бригадам использую следующие данные:

Бригада	Средняя заработная плата, руб, (x)	Фонд заработной платы, руб., (F)	Численность рабочих, чел, (f)



S	—

Меняя состав исходной информации, используемой для решения поставленной задачи, выделим 3 варианта ее решения.

Вариант 1. Вычислим среднюю заработную плату исходя из данных о фонде заработной платы и численности рабочих по логической формуле:

Средняя зарплата = Фонд зарплаты (по 3-м бригадам) .

(по 3-м бригадам) Численность рабочих (по 3-м бригадам)

Фонд зарплаты (по 3-м бригадам): SF=Sxf = 115100 руб.

Численность рабочих (в 3-х бригадах): Sf = 58 чел.

Средняя зарплата:

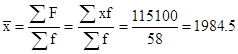средняя арифметическая взвешенная.

Вариант 2. Вычислим среднюю заработную плату исходя из данных о средней заработной плате и фонде заработной платы по каждой из бригад используя вышеприведенную логическую формулу.

Фонд зарплаты (по 3-м бригадам): SF= 115100 руб.

Численность рабочих (в 3-х бригадах): S(F/x) = 58 чел.

Средняя зарплата:

средняя гармоническая взвешенная.

Вариант 3. Вычислим среднюю заработную плату исходя из данных о средней заработной плате и численности рабочих по каждой из бригад.

Фонд зарплаты (по 3-м бригадам): Sxf .

Численность рабочих (в 3-х бригадах): Sf .

Средняя зарплата:

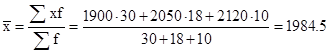средняя арифметическая взвешенная.

Средняя квадратическая применяется для расчета среднего квадратического отклонения и дисперсии, являющихся показателями вариации признаков.

Средняя геометрическая (простая) используется при вычислении среднего коэффициента роста (темпа роста) в рядах динамики.

12 Следующая ⇒