
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лекция по электродинамике 23.11.2020
Лекция по электродинамике 23.11.2020
9. Уравнения Максвелла для электростатики в среде. Диэлектрики. Свободные и связанные заряды
Электростатика в среде
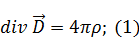
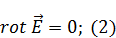

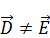
|

Возьмем от (4) дивергенцию:
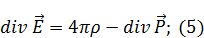
Источниками электрического поля в среде является не только заряды, но еще что-то в самой среде - 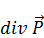 .
.
Из-за того, что среда/вещество помещено в электрическое поле в нем появляются какие-то дополнительные заряды. При помещении вещества в электрическое поле происходит смещение зарядов, так называемая поляризация. Из этой поляризации возникли дополнительные заряды. Они суммарно все равно дают нуль. Исходя из этих рассуждений можно заменить 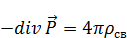 в выражении (5) и переписать в виде:
в выражении (5) и переписать в виде:
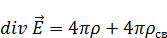
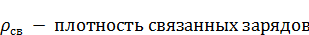
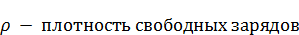
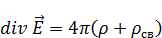
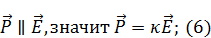
Подставим (6) в (4):
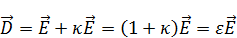
Найдем плотность связанных зарядов:
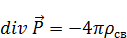
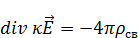
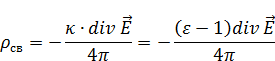
Электростатика в вакууме
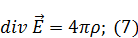
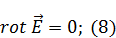
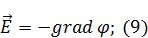
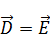
|
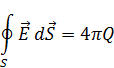
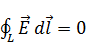 – это означает, что поле
– это означает, что поле 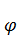 потенциально.
потенциально.
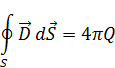
10. Граничные условия для полей 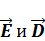

|
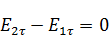
|
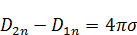
|
11. Диэлектрический шар в однородном электрическом поле
Диэлектрическая проницаемость шара:  .
.
Направим ось z по полю  .
.
Произвольная точка в сферической системе координат будет характеризоваться расстоянием 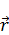 и углом
и углом 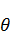 .
.

Потенциал зависит только от двух величин: 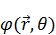
До того, как шар внесли поле и потенциал были такими:

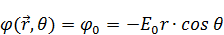
При внесении в поле диэлектрического шара:

Т. е. на больших расстояниях поле невозмущенное.
Внутри шара потенциал  вне шара
вне шара 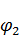 .
.
Из граничных условий для тангенциальных компонент следует:
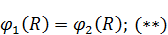
Для нормальной составляющей:
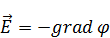
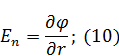
Запишем граничные условия для 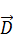 :
:
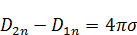
Т. к. на поверхности диэлектрика нет свободных зарядов, то:
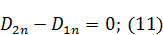
Зная, что 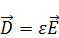 и учитывая (10) и (11):
и учитывая (10) и (11):
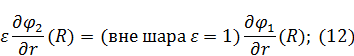
Первое, второе, третье граничные условия: (*), (**), (12).
В нуле потенциал не может быть равен бесконечности: 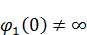 . Еще говорят, что не имеет особенностей.
. Еще говорят, что не имеет особенностей.
Решение для однородного поля: 
Решение для поля диполя: 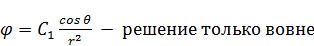 . Решение только вовне потому что в нуле будет бесконечность.
. Решение только вовне потому что в нуле будет бесконечность.

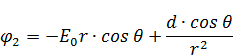
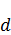 – дипольный момент шара, он возник из-за того, что поместили во внешнее однородное электрическое поле.
– дипольный момент шара, он возник из-за того, что поместили во внешнее однородное электрическое поле.
Нам неизвестно 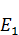 и
и 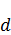 .
.
Напишем сразу ответ:
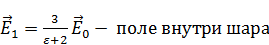 . Оно становится меньше, но все равно однородное.
. Оно становится меньше, но все равно однородное.
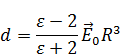
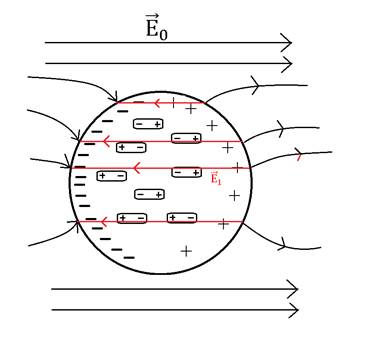
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|