Ряды распределения.

3. Ряды распределения.

Ряд распределения представляет собой упорядоченное расположение единиц изучаемой совокупности по группам в соответствии с выбранным группировочным признаком.

Основная цель построения рядов распределения заключается в выявлении основных свойств и закономерностей статистической совокупности.

Ряды распределения характеризуют состав (структуру) изучаемого явления, позволяют судить об однородности совокупности, границах ее изменения, закономерностях развития наблюдаемого объекта.

В зависимости от того, является ли признак взятый за основу группировки, качественным или количественным, различают соответственно два типа рядов распределения: атрибутивные и вариационные.

В зависимости от характера признака, положенного в основу группировки вариационные ряды подразделяют на дискретные и интервальные. Способы построения дискретного и интервального вариационных рядов различны.

В общем виде вариационный ряд распределения представляет собой таблицу, которая состоит из двух основных граф: варианты и частоты.

Варианта - это отдельное значение варьируемого признака, которое он принимает в ряду распределения.

Частота -количество той или иной варианты встречающейся в изучаемой совокупности.

В случае построения дискретного вариационного ряда распределения в первой графе указываются конкретные значения признака, во второй графе - численность единиц с определенным значением признака (т. е. частоту).

Для признака, имеющего непрерывное изменение, строится интервальный вариационный ряд. При его построении в первой графе отдельные значения признака указываются в интервалах “от - до”, во второй графе число единиц, входящих в интервал. Интервалы образуются, как правило, равные и закрытые.

В случае построения атрибутивного ряда распределения в первой графе указывают значения качественного признака, а во второй - число элементов совокупности, имеющих то или иное значение признака.

В ряде случаев, в зависимости от целей исследования, вариационный ряд распределения, состоящий из двух граф, иногда дополняется другими графами, необходимыми для вычисления отдельных статистических показателей. Достаточно часто в ряд вводится графа, в которой подсчитываются накопленные частоты (S).

Накопленные частоты- показывают, сколько единиц изучаемой совокупности имеют значение признака не больше, чем данное значение, и вычисляются путем последовательного прибавления к частоте первого интервала частот последующих интервалов.

Частоты ряда (f) могут быть заменены частостями (w), которые представляют собой частоты, выраженные в относительных числах (долях или процентах) и рассчитанные путем деления частоты каждого интервала на их общую сумму (или, что тоже самое, на объем совокупности):

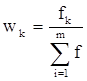Замена частот частостями позволяет сопоставить вариационные ряды с различным числом наблюдений.

Если вариационный ряд дан с неравными интервалами, то для правильного представления о характере распределения необходимо произвести расчет абсолютной или относительной плотности распределения.

Абсолютная плотность распределения (р) представляет собой величину частоту, приходящейся на единицу размера интервала отдельной группы ряда:

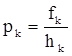Относительная плотность распределения (р’) - частное от деления частости отдельной группы на размер ее интервала:

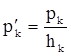При изучении рядов распределения часто прибегают к их графическому изображению. Такое представление ряда распределения облегчает его анализ и позволяет судить о форме распределения.

Дискретный вариационный ряд изображается в виде полигона распределения частот. Для изображения интервального ряда применяются полигон распределения частот и гистограмма частот. В случае неравенства интервалов гистограмма строится не по частотам или частостям, а по плотности распределения.

Графики строятся в прямоугольной системе координат.

В ряде случаев для изображения вариационных рядов используется кумулятивная кривая (кумулята), она особенно удобна для сравнения вариационных рядов.

Если поменять местами оси координат в кумуляте, то получаем новый вид графического изображения ряда распределения - огиву.

Пример.

Необходимо графически изобразить интервальный ряд распределения:

x	f	S
0 - 2
2 - 4
4 - 6
6 - 8
8 - 10
10 - 12

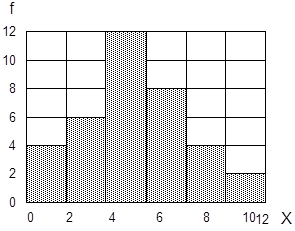
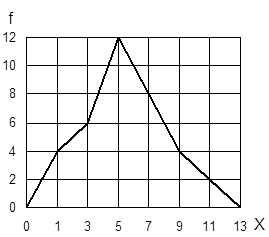
Гистограмма Полигон

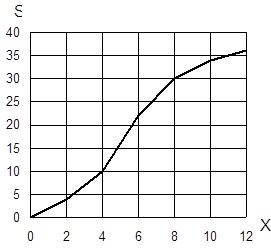
Кумулятивная кривая

Для анализа вариационных рядов используются три группы показателей:

* показатели центра распределения;

* показатели вариации (см. соответствующую тему);

* показатели формы распределения.

К показателям центра распределения относятся: средняя арифметическая, мода и медиана (см. тему: “Средние величины”).

⇐ Предыдущая 1 23