Метод группировки.

2. Метод группировки.

Под группировкойпонимают расчленение единиц изучаемой статистической совокупности на группы, однородные в каком-либо существенном отношении, и характеристику таких групп системой показателей.

С помощью метода группировок решаются следующие задачи:

* выделение социально-экономических типов явлений;

* изучение структуры явления и структурных сдвигов, происходящих в нем;

* выявление связи и зависимости между явлениями.

Статистические группировки по задачам, решаемым с их помощью, делятся на: типологические, структурные и аналитические.

Типологическая группировка - это разделение иследуемой качественно разнородной совокупности на классы, социально-экономические типы, однородные группы единиц в соответствии с правилами научной группировки. Примером типологической группировки является группировка промышленных предприятий по формам собственности.

Структурной называется группировка, в которой происходит разделение однородной совокупности на группы, характеризующие ее структуру по какому-либо варьирующему признаку. С помощью таких группировок могут изучаться: состав предприятий по численности занятых, стоимости основных фондов и т. д.

Аналитической группировкой называется группировка, которая выявляет взаимосвязи между изучаемыми явлениями и их признаками.

Группировка, в которой группы образованы по одному признаку, называется простой. Для характеристики явления бывает недостаточно разбить совокупность на группы по какому-то одному признаку. В этом случае строят сложные группировки.

Сложной называется группировка, в которой разделение совокупности на группы производится по двум и более признакам, взятым в сочетании.

Признак, на основе которого производится разбивка единиц совокупности на отдельные группы, называется группировочным признакомили основанием группировки.

В основание группировки могут быть положены как качественные, так количественные признаки.

При группировке по атрибутивному признаку число групп определяется количеством соотвествующих наименований, если число этих наименований не очень велико.

Если признак имеет большое количество разновидностей, то при группировке ряд наименований объединяют в одну группу. Для обосновния объединения их в группы разрабатываются классификации.

При группировке по количественному признаку число групп определяется в зависимости от хакрактера изменения признака и задач исследования.

Если количественный признак меняется дискретно, то число групп соответствует количеству значений признака.

Если количественныйпризнак меняется непрерывно, то группы образуют с помощью интервалов.

Интервал - это значения варьирующего признака, лежащие в определенных границах.

Нижней границей интервала называется наименьшее значение признака в интервале, а верхней границей - наибольшее значение признака.

Величина интервала - разность между верхней и нижней границами интервала.

Интервалы группировки могут быть закрытыми и открытыми.

Закрытые интервалы - это интервалы, имеющие как нижние, так и верхние границы.

Открытые интервалы - это интервалы, имеющие какую-либо одну границу - верхнюю или нижнюю.

На практике используется два вида интервалов: равные, неравные. Последние делятся на прогрессивно возрастающие, прогрессивно убывающие, произвольные и специализированные.

Равные интервалы используются в случае если признак меняется более или менене равномерно.

Величина равного интервала определяется по формуле:

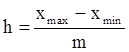где x_max, x_min - соответственно максимальное и минимальное значение признака в совокупности;

m - число групп.

Число групп может быть приближенно определено с помощью формулы Стерджесса:

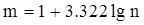где n - общее число единиц совокупности (объем совокупности).

Величину интервала обычно округляют до целого (всегда большего) числа.

Нижнюю границу первого интервала принимают равной минимальному значению признака(чаще всего его предварительно округляют до целого числа); верхняя граница первого интервала определяется как: (x_min+h). Для последующих групп границы определяются аналогично, т. е. последовательно прибавляется величина интервала.

Неравные интервалы применяются в статистике, когда значения признака меняются неравномерно и в значительных размерах. Неравные интервалы могут быть прогрессивно возрастающими или убывающими в арифметической или геометрической прогрессии.

Результаты сводки и группировки материалов статистического наблюдения оформляются в виде статистических таблиц и рядов распределения.

Группировки, построенные за один и тот же период времени, но для разных регионов или, наоборот, для одного региона, но за два разных периода времени, могут оказаться несопоставимыми из-за различного числа выделенных групп или неодинаковости границ интервалов. Для того, чтобв привести такие группировки к сопоставиму виду, используется метод вторичной группировки. Суть метода состоит в перегруппировке единиц объекта без обращения к первичным данным.

Вторичная группировка - операция по образованию новых групп на основе ранее построенной группировки.

Применяют два способа образования новых групп.

Метод объединения первоначальных интервалов, является наиболее простым и распространенным методом, и применяется в случае перехода от мелких к более крупным интервалам, когда границы новых и старых интервалов совпвадают.

Метод долевой перегруппировки состоит в образовании новых групп на основе закрепления за каждой группой определенной доли единиц совокупности.

⇐ Предыдущая 123 Следующая ⇒