Квадрупольный момент

7. Квадрупольный момент

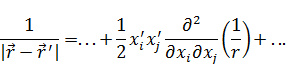
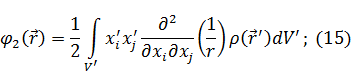
- тензор квадрупольного момента; (*).

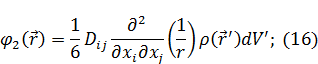
Покажем, что (15) совпадает с (16):

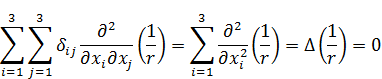
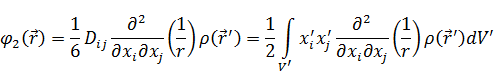
Вычислим в (16) выражение :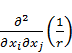

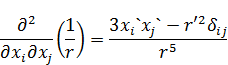
И тогда потенциал второго порядка малости будет выглядеть следующим образом:

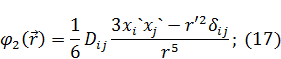
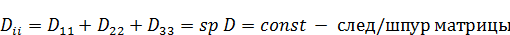
Почему берут только диагональные элементы. В тензорном анализе доказывается, что при любом преобразовании/повороте след матрицы не меняется.

Найдем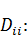

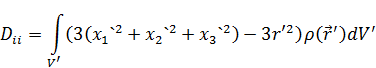
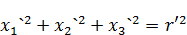
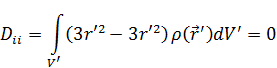
Шпур тензора квадрупольного момента равен нулю 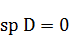. Это главная причина, по которой был выбрано выражение (*) для тензора квадрупольного момента.

Можно упростить выражение для потенциала второго порядка малости (17):

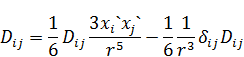
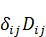– это на самом деле 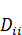, а это есть след матрицы.

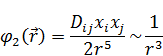
Когда мы работаем с дипольным моментом? Когда общий заряд системы равен нулю. Квадрупольный момент используется, когда дипольный момент равен нулю.