Контакты

Случайная статья

Лекция по электродинамике 02.11.2020

Стр 1 из 2Следующая ⇒

Лекция по электродинамике 02.11.2020

6. Мультипольное разложение

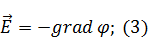
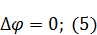
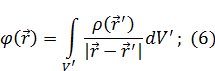
Разложим функцию в точке :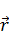

Вычисляем производные в той точке, где нам нужен потенциал, а не в той точке, где находится заряд. Заряд находится в штрихованной системе.

В выражении (7) идет немое суммирование.

Применим (7) для общего решения уравнения Пуассона (6). Применяется он не ко всему интегралу, а только там, где встречается 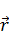. Здесь мы пользуемся тем, что
.

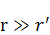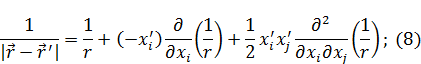
Потенциал тогда будет выглядеть следующим образом:

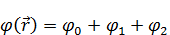
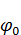– приближение нулевого порядка малости;

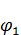– приближение первого порядка малости;

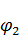- приближение второго порядка малости.

Тогда с учетом разложения потенциал нулевого порядка малости будет иметь вид:

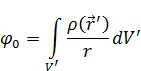
– не зависит от интегрирования. И тогда:

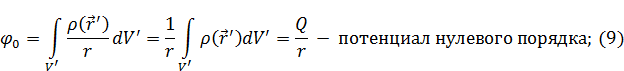
Выражение получилось точно такое, что и для потенциала точечного заряда.

Найдем потенциал первого порядка малости:

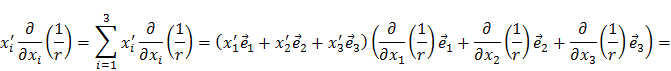
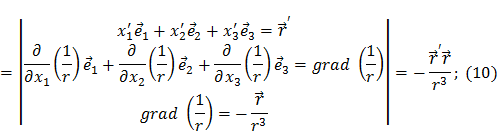
С учетом минуса в выражении (8) для потенциала первого порядка малости будет равно:

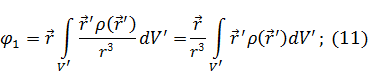
Что такое 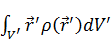? Когда вектор умножается на некую величину из механики это будет момент. Это будет называться дипольным моментом системы зарядов:

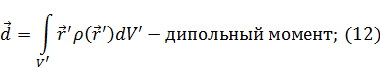
Учитывая (12), выражение (11) примет вид:

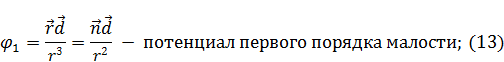
Найдем потенциал второго порядка малости:

Чему будет равен дипольный момент, если мы переместим начало координат. Зависит ли дипольный момент от выбора начала координат?

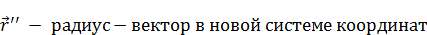
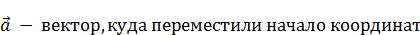
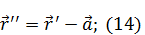
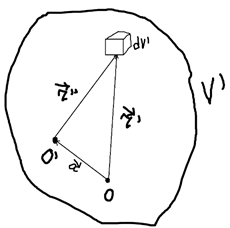
Дипольный момент в новой системе координат:

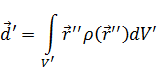
Учитывая (14), придем к:

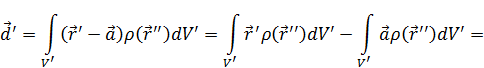
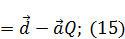
Можно подобрать такое начало координат, при котором 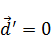. Если 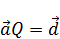, то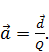

Найдем напряженность для нулевого и первого порядка малости по формуле (3).

Потенциал второго приближения выглядит:

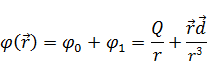
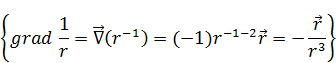
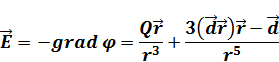
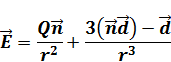
Рассмотрим потенциал первого порядка малости:

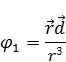
Если направить ось z по направлению дипольного момента, то формула будет выглядеть следующим образом:

12 Следующая ⇒

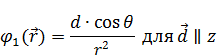
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.