Контакты

Случайная статья

Лекция по электродинамике. 7.12.2020

Стр 1 из 2Следующая ⇒

Лекция по электродинамике. 7.12.2020

Постоянное магнитное поле

14. Уравнения Максвелла для стационарного магнитного поля в вакууме. Сила Лоренца (здесь его нет). Вектор-потенциал для магнитного поля. Уравнениедля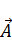

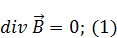
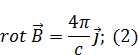
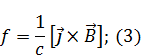
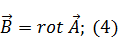
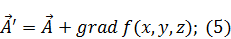
Возьмем ротор от выражения (5):

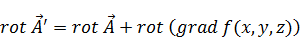
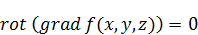
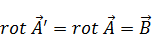
Вспомним, тоже самое можно проделать со скалярным потенциалом:

Возьмем градиент от выражения (6):

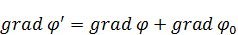
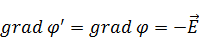
Калибровку для скалярного потенциала мы задавали таким образом, ставили точку, в которой потенциал равен нулю, это обычно было бесконечность:

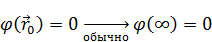
Для постоянного магнитного поля мы делаем кулоновскую калибровку:

Подставив (4) в (2) мы получали (при выводе пользовались кулоновской калибровкой):

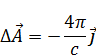
Лапласиан для вектора, это все равно, что записано для компонент:

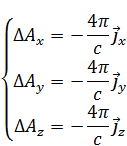
15. Общее решение уравнения для . Закон Био-Савара

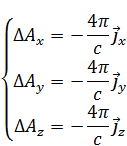
Решение этой системы:

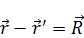
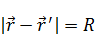
Рисунок. Система токов.

Если ввести элементарный векторный потенциал:

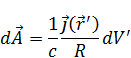
Суммируя, можно получить единый потенциал (7).

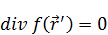
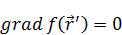Потому что производные по нештрихованной берутся.

Найдем дивергенцию (7) по нештрихованной системе:

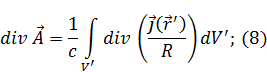
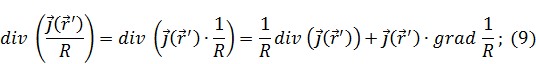
т. к. , подставляя это в (9), получаем:

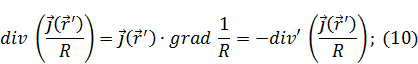
Выражение (10) подставим в (8):

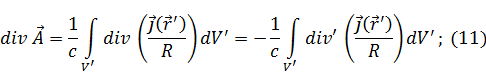
Применим теорему Остроградского-Гаусса для (11):

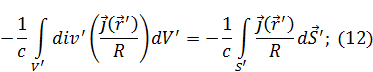
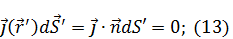
Подставим (13) в (12):

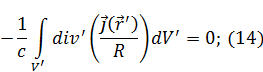
Подставим (14) в (11):

– нормировка Кулона выполняется.

Закон Био-Савара

Найдем 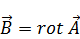, подставляя вместо 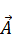(7):

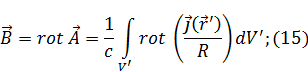
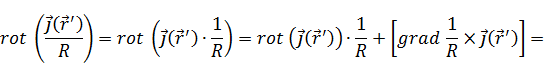
Подставим (15) в (16):

- Закон Био-Савара.

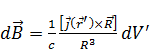- Закон Био-Савара в дифференциальной форме.

16. Поток и циркуляция магнитного поля. Граничные условия для вектора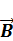

Граничные условия для постоянного магнитного поля

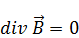
Нормальная составляющая не терпит разрыв на границе двух сред:

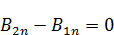
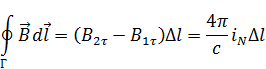
– поверхностная плотность токов в направлении .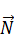

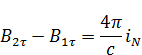
Запишем в векторной форме:

12 Следующая ⇒

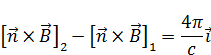
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.