Контакты

Случайная статья

Найти значения функции в точках экстремума.

⇐ ПредыдущаяСтр 2 из 2

!!! Найти значения функции в точках экстремума.

6. По данным исследования построить график функции.

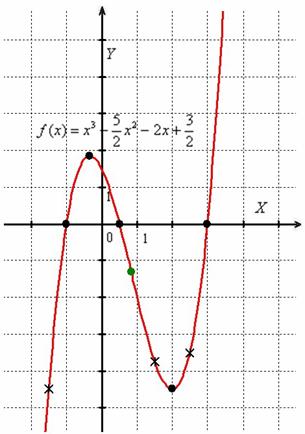
Пример 1. Исследовать функцию и по результатам исследования построить график.

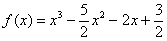
Решение.

1) D(f): R

2) Проверим функцию на чётность/нечётность:

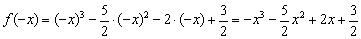
, значит, данная функция не является чётной или нечётной.

Функция непериодическая.

3) Нули функции.

С осью Оy:

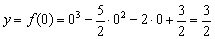
Чтобы найти точки пересечения с осью Ox (нули функции) требуется решить уравнение f(x) = 0:

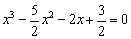
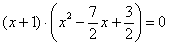
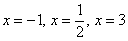
4) Таким образом, на интервалах график расположен ниже оси абсцисс f(x)<0, а на интервалах 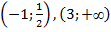– выше данной оси f(x) >0.

5) Возрастание, убывание.

Найдём критические точки:

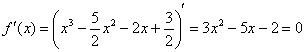
Отложим их на числовой прямой и определим знаки производной:
1
Следовательно, функция возрастает на 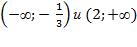и убывает на .

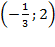Экстремумы функции

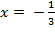точка максимума, так как при переходе через нее производная меняет знак с «+» на «-». 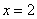точка минимума, так как при переходе через нее производная меняет знак с «-» на «+».

.

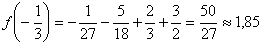
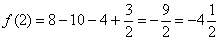6) Строим график функции.

Алгоритм нахождения наибольшего или наименьшего значения функции на отрезке:

Найти производную функции.
Определить критические точки (те точки, в которых производная функции обращается в ноль или не существует).
Выбрать из найденных точек те, которые принадлежат данному отрезку.
Вычислить значения функции (не производной!) в этих точках и на концах отрезка.
Среди полученных значений выбрать наибольшее или наименьшее, оно и будет искомым.

Пример2 . Найдите наименьшее значение функции y = x³ – 18x² + 81x + 23 на отрезке [8; 13].

Решение:действуем по алгоритму нахождения наименьшего значения функции на отрезке:

1) y’ = 3x² – 36x + 81.

2) y’ = 3x² – 36x + 81 = 0

x² – 12x + 27 = 0,

x = 3 и x = 9

3) x = 9 [8; 13].

4) y = x³ – 18x² + 81x + 23 = x(x-9)²+23:

o y(8) = 8 · (8-9)²+23 = 31;

o y(9) = 9 · (9-9)²+23 = 23;

o y(13) = 13 · (13-9)²+23 = 231.

Ответ. ;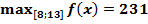

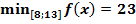
⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.