
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
КОЧЕТОВА ЭЛЕОНОРА ФЕДОРОВНА 2 страница
Из рисунка 7 видно, что истинные азимуты одной и той же линии в различных ее точках отличаются на величину γ, а прямой и обратный азимуты – на (180˚+γ).
Магнитные азимуты линий есть горизонтальные углы, отсчитываемые от северного направления магнитного меридиана или линии ему параллельной по ходу часовой стрелки до направления заданной линии местности. Направление магнитного меридиана определяется магнитной стрелкой, оно не совпадает с направлением истинного меридиана в данной точке на угол δ, называемый склонением магнитной стрелки. Склонение может быть западным (-) и восточным (+), в пределах России δ меняется от 0˚до ±15˚.
Существует связь между истинным и магнитным азимутами: Аист.=Амаг.+δ. Все вышесказанное об истинных азимутах в равной мере относится и к магнитным азимутам.
Дирекционный угол есть горизонтальный угол, отсчитываемый по ходу часовой стрелки от северного направления осевого меридиана или линии, ему параллельной, до направления данной линии местности. Изменяется он от 0˚ до 360˚. Дирекционные углы одной и той же линии в различных ее точках одинаковы, а прямые и обратные дирекционные углы всегда отличаются ровно на 180˚ (рис. 8): α=αс= αД; αД΄=α+180˚; αс΄=αД+180˚….Поэтому – то на практике используется именно α.
 |  |  | |||
 А
А

 αс
αс

 αД
αД
 С
С
 αс΄ αЕ
αс΄ αЕ

 Д
Д
 αД΄ В
αД΄ В
Е αЕ'
Рис. 8
Поскольку меридианы в различных точках не параллельны и сходятся к полюсам, то их направления, выраженные полуденными линиями, тоже не будут параллельны. Этот угол между полуденными линиями называется в геодезии сближением меридианов γ. Оно может быть западным (в точке С) и восточным (в точке Д). В пределах зоны оно не может быть более 3˚. Условились считать, что γвост.+, γзап.-.В пределах координатной зоны линии, параллельные осевому меридиану, не совпадают с географическими меридианами, а образуют с ними некоторый угол, называемый гауссовым сближением меридианов. В восточной половине зоны линии, параллельные осевому меридиану, отклоняются к востоку от географического меридиана, сближение называется восточным и обозначается знаком «плюс». В западной половине зоны линии - отклоняются к западу от географического меридиана, сближение называется западным и обозначается знаком «минус».
 |
γ=Δλ·sinφ φ=0˚ на экваторе
φ=90˚ на полюсе
В пределах 6˚-ой зоны γmах=3˚.
Румбом линии называется острый горизонтальный угол, отсчитываемый от ближайшего направления меридиана – северного или южного до направления линии местности. В зависимости от используемого меридиана румбы бывают истинные, магнитные и осевые. Они изменяются от 0˚ до 90˚ и имеют названия по сторонам света (четвертям): СВ, ЮВ, ЮЗ, СЗ. Прямой и обратный румбы в данной точке равны по величине, но противоположны по наименованию. Истинные и магнитные румбы отличаются, кроме того, на величину склонения и сближения меридианов, как и азимуты.
От азимутов и дирекционных углов можно переходить к румбам и обратно,
используя очевидные формулы (рис. 9):
СВ: r=α
ЮВ: r=180˚-α
ЮЗ: r=α-180˚
СЗ: r=360˚-α.
 360º С 0º СВ
360º С 0º СВ

 α
α
СЗ r

 r
r
 |
 α 90º В
α 90º В

 З
З
 270º α
270º α
α
ЮЗ r r
ЮВ
180º
Рис. 9
4. Связь дирекционных углов и горизонтальных углов полигона
 β1'
β1'


 1
1

 β1
β1
 2 β2'
2 β2'
β5 β  2
2
 β5' 5
β5' 5
 |
β4 β 
 3 3 β3'
3 3 β3'
β4' 4
Рис. 10
Ломаная линия с закрепленными на местности точками излома и с измеренными длинами сторон и горизонтальными углами называется полигоном. Полигоны могут быть разомкнутые и замкнутые (на рис.10 замкнутый полигон). Точки полигона закрепляют временными знаками – деревянными кольями.
β1, β2…-внутренние углы – правые; β1´, β2´…- внешние углы – левые.
Зная дирекционный угол одной стороны полигона, можно всегда вычислить по горизонтальным углам дирекционные углы всех остальных сторон.
α1-2 – дано, β1, β2…-измерены.
 |
 α1-2
α1-2




 2 α2-3
2 α2-3
 3 α2-3
3 α2-3

 β2
β2
 α1-2 α3-4
α1-2 α3-4
β3
 1
1
β1 на т. 4
Рис. 11
Из рисунка 11 видно, что α2-3= α1-2 +180˚ - β2
α3-4= α2-3 +180˚ - β3
……………………
αn= αn-1 +180˚ - βn - формула для правых углов.
Так как βправ.=360˚-β´лев., то для левых углов αn= αn-1 + βn´-180˚.
5. Прямая и обратная геодезические задачи
Прямая геодезическая задача заключается в том, что по известным координатам одной точки, дирекционному углу и расстоянию до другой определяют координаты последней. При вычислениях чаще всего дирекционные углы переводят в румбы. Прямая геодезическая задача решается и при вычислении координат вершин полигонов.
Дано: х1; у1 – координаты начальной точки; α1-2; α2-3; α3-4; α4-5; α5-1 - дирекционные углы сторон полигона. d1-2; d2-3………………..d5-1 - горизонтальные проложения сторон полигона. Найти: х2 и у2; х3 и у3…………..х5 и у5. Разница между координатами соседних точек называется приращением координат: х2 – х1=Δх1; у2 – у1=Δу1. Отсюда
х2=х1+Δх1; у2=у1+Δу1. Из треугольника следует (рис. 21): Δх1=d1-2∙cosr1-2;
Δу1= d1-2∙sinr1-2.
Из рисунка 22 следует: х3=х2+Δх2; у3=у2+Δу2;
Δх2=d2-3∙cosr2-3; Δу2= d2-3∙ sinr2-3. Перейдем к общему случаю: хn=хn-1+Δхn;
уn =уn-1+Δуn; Δхn= dn∙cosrn; Δуn= dn sinrn.
При вычислениях учитываются знаки приращений координат в зависимости от четверти, в которую направлена линия (см. выше). Если вместо румбов использовать дирекционные углы, то знаки перед приращениями координат получаются сами собой.
 Х
Х
 2
2
2


 3
3
1 Δх1-2 1
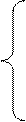

 х2
х2
х1
Δу1-2
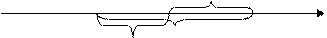 |
4 у2 У
5 у1
Рис. 21
 Х
Х


 2
2
Δх2-3
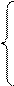

 3
3
х3
Δу2-3
 х2
х2
 |
У
у2 у3
Рис. 22
Координаты n – ой точки полигона можно выразить и через координаты первой точки.
х2=х1+Δх1
х3=х2+Δх2=х1+ (Δх1+ Δх2)
х4=х3+Δх3= х1+ (Δх1+ Δх2+ Δх3)
х5=х4+Δх4= х1+ (Δх1+ Δх2+ Δх3+Δх4)
……………………………………………
хn= х1+ 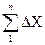 и уn=у1+
и уn=у1+ 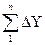 ;
;

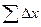 и
и 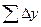 - здесь суммы приращений координат. Отсюда запишем:
- здесь суммы приращений координат. Отсюда запишем:
хn - х1= 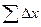
уn – у1= 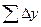 .
.
В случае замкнутого полигона, когда, обойдя все вершины поочередно, мы возвращаемся в исходную, хn - х1=0 и уn – у1=0. Следовательно, для замкнутого полигона сумма приращений координат по обеим осям равна нулю.
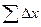 теор.=0 и
теор.=0 и 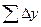 теор.=0.
теор.=0.
Однако в связи с ошибками в угловых и линейных величинах эта сумма будет несколько отличаться от 0. Мы возвратимся не в точку 1, а в 1΄ (см. рис. 23).
Полученная разница в суммах приращений координат называется невязкой.
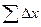 изм.=fх≠0 – невязка по х;
изм.=fх≠0 – невязка по х;
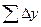 изм.=fу ≠0 – невязка по у.
изм.=fу ≠0 – невязка по у.
Для оценки точности полигона вычисляют абсолютную невязку:
(1 - 1΄)=fабс.= 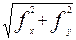 ,
,
а затем относительную ошибку:
fотн.= 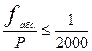 ; Р – периметр.
; Р – периметр.


 Х 2
Х 2
fу


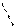 1
1
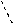
 fабс. fх 3
fабс. fх 3
 1'
1'
 |
5 4

У
Рис. 23
Если условие неравенства выполняется, полученную невязку по осям координат распределяют в вычисленные приращения в виде поправок, с обратным невязке знаком, пропорционально значениям горизонтальных проложений: большую поправку в большее значение проложения.
Обратная геодезическая задача заключается в вычислении дирекционного угла и горизонтального проложения линии, по известным координатам ее начальной и конечной точек. Из предыдущих рисунков видно, что
d= 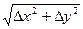 ; tgr=
; tgr= 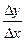 ; r=arctgr; d=
; r=arctgr; d= 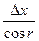 =
= 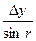 .
.
Дирекционный угол находят по полученному румбу, учитывая четверть, в которую направлена прямая. Четверть определяется по знакам приращений координат:
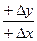 1 четверть α=r;
1 четверть α=r; 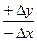 2 четверть α=180° - r;
2 четверть α=180° - r;

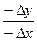 3 четверть α=r+180°;
3 четверть α=r+180°; 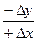 4 четверть α=360° - r.
4 четверть α=360° - r.
6.Топографические карты и планы
6.1. Понятие о плане, карте, профиле

 План есть уменьшенное и подобное изображение на бумаге горизонтальной проекции сравнительно небольшого участка местности. Размеры участка до 25 км2 – в этом случае не учитывается кривизна Земли. Степень уменьшения изображения сравнительно небольшая: 100, 200, 500…5000раз. Для удобства пользования на планах наносится координатная сетка. Планы могут быть: горизонтальными (контурными) высотными и контурно – высотными (топографическими).
План есть уменьшенное и подобное изображение на бумаге горизонтальной проекции сравнительно небольшого участка местности. Размеры участка до 25 км2 – в этом случае не учитывается кривизна Земли. Степень уменьшения изображения сравнительно небольшая: 100, 200, 500…5000раз. Для удобства пользования на планах наносится координатная сетка. Планы могут быть: горизонтальными (контурными) высотными и контурно – высотными (топографическими).
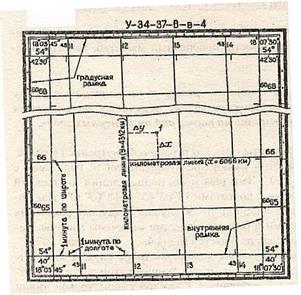
координатная сетка километровая сетка
План М 1:1000 Карта М 1:10000
Рис. 12
Карта – уменьшенное и закономерно искаженное вследствие влияния кривизны Земли изображение на бумаге горизонтальной проекции значительной части или всей земной поверхности. Степень уменьшения больше по сравнению с планом: 10000 раз, 50000….. . Искажения происходят из–за невозможности развертывания сферических поверхностей (геоид, эллипсоид) в плоскость (бумага плоская) без разрывов и складок. На картах наносят градусные и километровые сетки. Все карты контурно – высотные (топографические).
Профиль местности есть линия пересечения земной поверхности с отвесной (вертикальной) плоскостью, расположенной в заданном направлении (PQ) (рис. 13). Его уменьшенное изображение на бумаге также называется профилем. Направление сечения может быть прямолинейным, ломаным или криволинейным.
 |






 Р
Р
 |  | ||



 Q
Q
 |  | ||
Рис.13
По планам и картам можно решать ряд задач:
1. Определение расстояний между точками.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|